Midsegment of a Triangle
A closed figure made with 3 line segments forms the shape of a triangle.
Let us explore the world of triangle
Triangle has many subparts. Such as, angles, sides, median, midpoint, midsegment, etc. Here's an activity for you. You can now visualize various types of triangles in math based on their sides and angles. Try changing the position of the vertices to understand the relationship between sides and angles of a triangle.
In the later part of this chapter we will discuss about midpoint and midsegments of a triangle.
Given any two points, say \(A\) and \(C\), the midpoint is a point \(B\) which is located halfway between the points \(A\) and \(B\).

Observe that the point \(B\) is equidistant from \(A\) and \(C\).
A midpoint exists only for a line segment.
Line which connects the midpoint is termed as midsegment.
In this mini-lesson, we will explore the world of midsegment of a triangle by finding the answers to the questions like what is midsegment of a triangle, triangle midsegment theorem, and proof with the help of interactive questions.
So let's get started!
Lesson Plan
What Is Midsegment of a Triangle?
Midsegment of a Triangle Definition
A midsegment of a triangle is a line segment that joins the midpoints or center of two opposite or adjacent sides of a triangle

In the above figure, D is the midpoint of AB and E is the midpoint of AC.
Here DE is a midsegment of a triangle ABC.
Triangle Midsegment Theorem
The midsegment theorem states that a line segment connecting the midpoints of any two sides of a triangle is parallel to the third side of a triangle and is half of it.

In the triangle ABC we have,
\(AD=DB\) and \(AE=EC\)
Then according to the midsegment theorem
\(DE∥BC\) and \(DE=\dfrac{1}{2}\ BC\)
Similarly,
\(AD=DB\) and \(BF=FC\)
Then according to the midsegment theorem
\(DF∥AC\) and \(DF=\dfrac{1}{2}\ AC\)
Similarly,
\(AE=EC\) and \(BF=FC\)
Then according to the midsegment theorem
\(EF∥AB\) and \(EF=\dfrac{1}{2}\ AB\)
Proof for Midsegment of a Triangle
In the above section, we saw a triangle \(ABC\), with \(D,\) \(E,\) and \(F\) as three midpoints.
We need to prove two things to justify the proof of the triangle midsegment theorem:
- \(DE∥BC\)
- \(DE=\dfrac{1}{2}\ BC\)

Given: D and E are the midpoints of AB and AC
To prove, \(DE∥BC\) and \(DE=\dfrac{1}{2}\ BC\) we need to draw a line parallel to AB meet E produced at F.
In \(\bigtriangleup{ADE}\) and \(\bigtriangleup{CFE}\)
\(\begin{align} AE &=EC\text{ (E is the midpoint of AC)}\\\ \angle{1} &=\angle{2}\text{ (Vertically opposite angles)}\\\ \angle{3} &=\angle{4}\text{ (Alternate angles)}\end{align}\)
By AAS congruency of triangle we have,
\(\bigtriangleup{ADE} \cong \bigtriangleup{CFE}\)
By CPCT we have,
\(DE=FE\)
\(AD=CF\)
D is the midpoint of AB
\(AD=BD\)
\(BD=CF\)
DBCF is a parallelogram,
\(DF || BC\) and \(DF = BC\)
\(DE || BC\) and \(DF = BC\)
\(DE=\dfrac{1}{2}DF\)
since, DF = BC
\(DE=\dfrac{1}{2}BC\)
Hence Proved
Midsegment of a Triangle Formula
| Midsegment \(=\) \(\dfrac{1}{2}\times\) Triangle Base |
What Is the Converse of the Triangle Midsegment Theorem?
The converse of the midsegment theorem is defined as: When a line segment connects two midpoints of two opposite sides of a triangle and is parallel to the third side of a triangle and is half of it then it is a midsegment of a triangle.

In triangle ABC we have,
\(DE∥BC\) and \(DE=\dfrac{1}{2}\ BC\)
Then according to the converse of the triangle midsegment theorem
\(AD=DB\) and \(AE=EC\)
\(DE\) is a midsegment of triangle \(ABC\)
Proof for Converse of the Triangle Midsegment Theorem
In the above section, we saw \(\bigtriangleup{ABC}\), with \(D,\) \(E,\) and \(F\) as three midpoints.
We need to prove any one of the things mentioned below to justify the proof of the converse of a triangle midsegment theorem:
- \(DE\) is a midsegment of a \(\bigtriangleup{ABC}\)
- \(AD=DB\) and \(AE=EC\)

We have D as the midpoint of AB, then \(AD = DB\) and \(DE||BC\)
\(AB\) \(=\) \(AD + DB\) \(=\) \(DB + DB\) \(=\) \(2DB\)
DBCF is a parallelogram.
\(DE||BC\) and \(BD||CF\)
Opposite sides of a parallelogram are equal.
\(BD=CF\)
\(DA=CF\)
In \(\bigtriangleup{ADE}\) and \(\bigtriangleup{CFE}\)
\(\begin{align}\angle{1} &=\angle{2}\text{ (Vertically opposite angles)}\\\ \angle{3} &=\angle{4}\text{ (Alternate angles)}\\\ DA &=CF\end{align}\)
By AAS congruency of triangle we have,
\(\bigtriangleup{ADE} \cong \bigtriangleup{CFE}\)
By CPCT we have
\(AE=EC\)
E is the midpoint of AC and DF.
Hence, DE is a midsegment of \(\bigtriangleup{ABC}\).

a) The line segment through a midpoint is always parallel to one side of the triangle.
b) The midsegment \(=\) \(\dfrac{1}{2}\) the length of the third side of a triangle.
c) A triangle can have a maximum of three midsegments.
d) The midsegment of a triangle theorem is also known as mid-point theorem.
Solved Examples
To understand the midsegment of a triangle better, let us look at some solved examples.
| Example 1 |
In the given figure H and M are the midpoints of triangle EFG. Help Jamie to prove \(HM||FG\) for the following two cases.
a) EH = 6, FH = 9, EM = 2 and GM = 3
b) EH = 16, FH = 12, EM = 4 and GM = 3

Solution
a) We have EH = 6, FH = 9, EM = 2, and GM = 3
\(\dfrac{EH}{FH}=\dfrac{6}{9}=\dfrac{2}{3}\)
\(\dfrac{EM}{GM}= \dfrac{EH}{FH}=\dfrac{2}{3}\)
b) We have EH = 16, FH = 12, EM = 4, and GM = 3
\(\dfrac{EH}{FH}=\dfrac{16}{12}=\dfrac{4}{3}\)
\(\dfrac{EM}{GM}= \dfrac{EH}{FH}=\dfrac{4}{3}\)
HM divides EF and EG of triangle EFG in equal ratios.
Hence, HM is the midsegment of triangle EFG.
|
\(\therefore\) \(HM || FG\) |
| Example 2 |
Help Ron in finding the value of x and the value of line segment AB, given that A and B are midpoints of triangle PQR.

Solution
We have two midpoints A and B.
According to the midsegment triangle theorem
\(\begin{align}QR &=2AB\\\
36 &=2(9x)\\\
x &=2\\\
AB &=18\end{align}\)
| \(\therefore\) The value of x is 2 The value of AB is 18 |
Interactive Questions
Here are a few activities for you to practice. Select/Type your answer and click the "Check Answer" button to see the result.

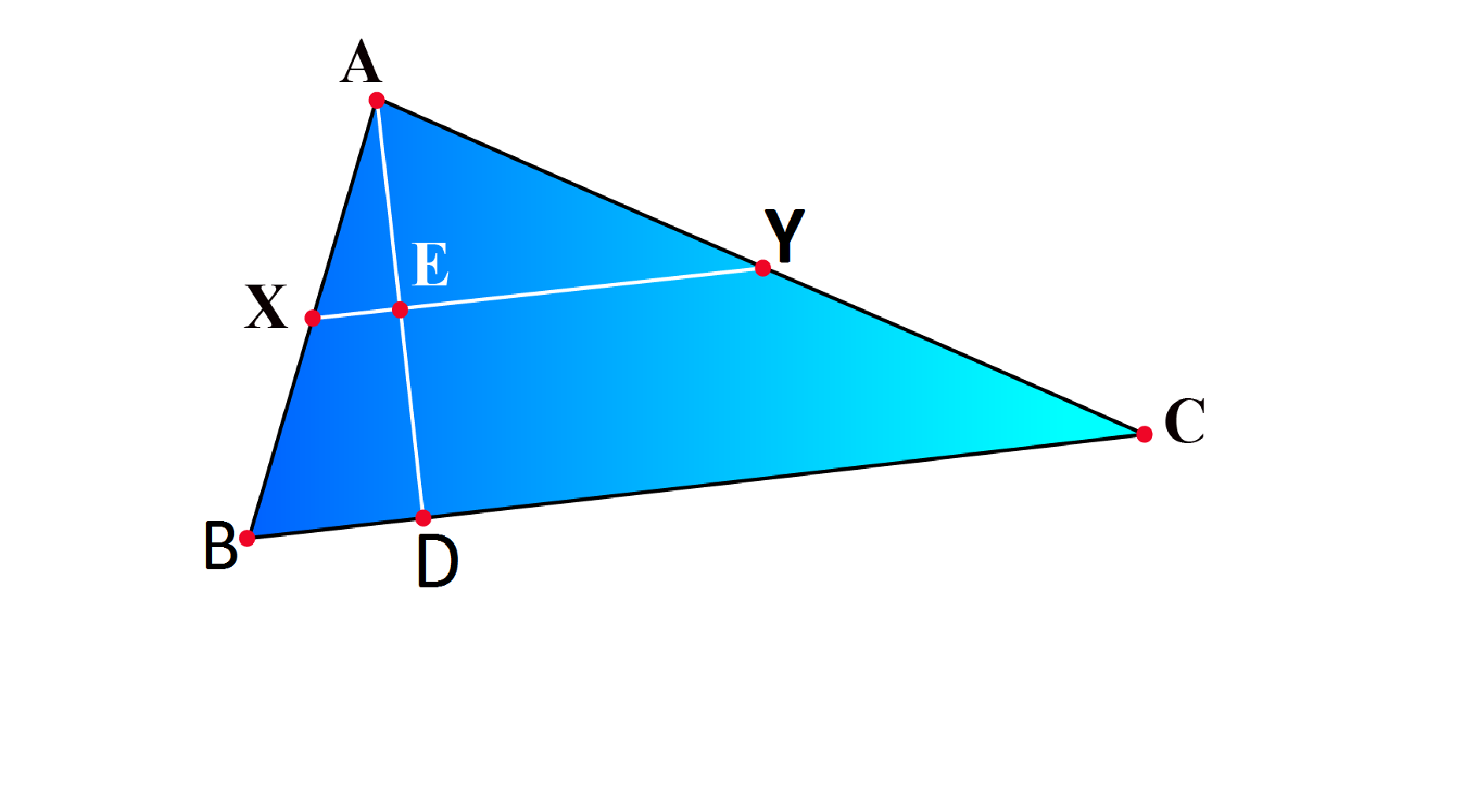
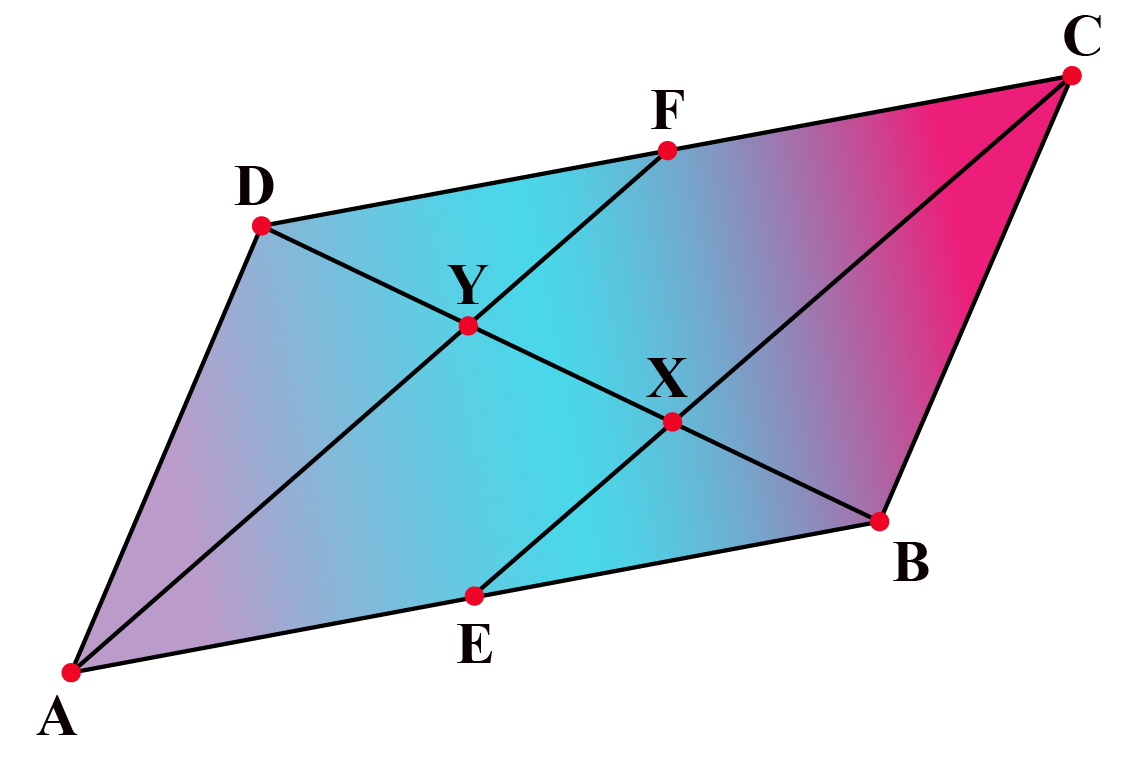
Let's Summarize
The mini-lesson targeted the fascinating concept of the midsegment of a triangle. The math journey around the midsegment of a triangle starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever. Here lies the magic with Cuemath.
About Cuemath
At Cuemath, our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.
Frequently Asked Questions(FAQ's)
1. What is the midsegment of a triangle?
A midsegment of a triangle is a line segment that joins the midpoints or center of two opposite or adjacent sides of a triangle
In a triangle, we can have 3 midsegments.

In the above figure, D is the midpoint of AB and E is the midpoint of AC, and F is the midpoint of BC.
Here DE, DF, and EF are 3 midsegments of a triangle ABC.
2. How to find the midsegment of a triangle?
We can find the midsegment of a triangle by using the midsegment of a triangle formula,
Midsegment \(=\) \(\dfrac{1}{2}\times\) Triangle Base.
3. What is the midpoint theorem?
The midpoint theorem states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the third side. Consider an arbitrary triangle, \(\bigtriangleup{ABC}\). Let D and E be the midpoints of AB and AC. Suppose that you join D and E:
The midpoint theorem says that DE will be parallel to BC and equal to exactly half of BC.
