Midpoint Formula
Midpoint refers to a point that is exactly in the middle of the line segment joining two points. The two reference points are the endpoints of a line segment, and the midpoint is lying in between the two points. The midpoint divides the line joining these two points into two equal halves. Further, if a line is drawn to bisect a line segment joining these two points, the line passes through the midpoint.
The midpoint formula is used to find the midpoint between two points whose coordinates are known to us. The midpoint formula is also used to find the coordinates of the endpoint if we know the coordinates of the other endpoint and the midpoint. In the coordinate plane, if a line is drawn to connect two points (4, 2), and (8, 6), then the coordinates of the midpoint of the line joining these two points are ({4 + 8}/2, {2 + 6}/2) = (12/2, 8/2) = (6, 4). Let us learn more about the formula of the midpoint, and different midpoint methods.
| 1. | What is Midpoint? |
| 2. | Midpoint Formula |
| 3. | How to Find Midpoint? |
| 4. | Formulas Related to Midpoint |
| 5. | FAQs on Midpoint Formula |
What is Midpoint?
A midpoint is a point lying between two points and is in the middle of the line joining the two points. If a line is drawn joining the two points, then the midpoint is a point at the middle of the line and is equidistant from the two points. Given any two points, say A and C, the midpoint is a point B which is located halfway between points A and C. Therefore, to calculate AB or BC, we can simply measure the length of the line segment and divide by 2.

Observe that point B is equidistant from A and C. A midpoint exists only for a line segment. A line or a ray cannot have a midpoint because a line is indefinite in both directions and a ray has only one end and thus can be extended.
Midpoint Formula
The midpoint formula is defined for the points in the coordinate axes. Let (x1, y)1 and (x2, y)2 be the endpoints of a line segment. The midpoint is equal to half of the sum of the x-coordinates of the two points, and half of the sum of the y-coordinates of the two points. The midpoint formula to calculate the midpoint of a line segment joining these points can be given as,
Midpoint Formula in Math
Given two points A (x1, y1) and B (x2, y2), the midpoint between A and B is given by,
M(x3, y3) = ((x1 + x2)/2, (y1 + y2)/2)
where, M is the midpoint between A and B, and (x3, y3) are its coordinates.
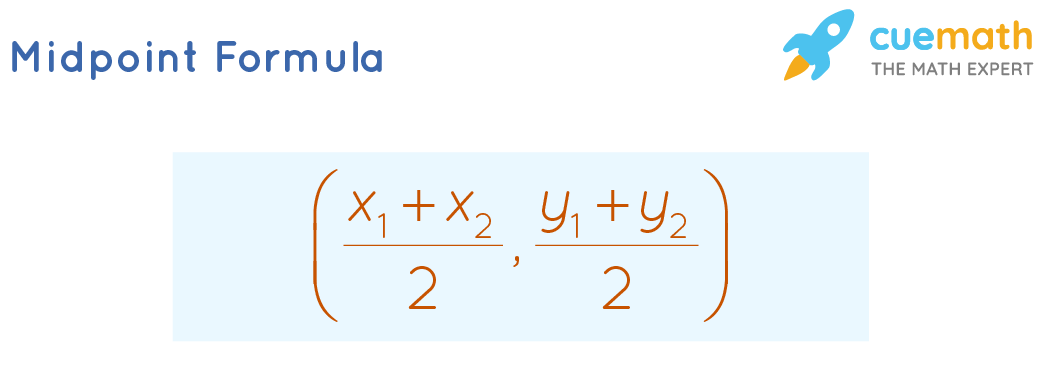
Derivation of Midpoint Formula
Let us look at this example and find the midpoint of two points in one-dimensional axis. Suppose, we have two points, 5 and 9, on a number line. The midpoint will be calculated as: (5 + 9)/2 = 14/2 = 7. So, 7 is the midpoint of 5 and 9.

We would apply the same logic to find the midpoint of a line segment with its endpoints, (x1, y1) and (x2, y2) on a coordinate plane. For any line segment, the midpoint is halfway between its two endpoints. The expression for the x-coordinate of the midpoint is [x1 + x2]/2, which is the average of the x-coordinates. Similarly, the expression for the y-coordinate is [y1 + y2]/2, which is the average of the y-coordinates.
Thus, the formula for midpoint is, ((x1 + x2)/2, (y1 + y2)/2)
Let us check an example to see the application of the midpoint formula.
Example: Using the midpoint formula, find the midpoint between points X(5, 3) and Y(7, 8).
Solution: Let M be the midpoint between X and Y.
M = ((5 + 7)/2, (3 + 8)/2) = (6, 11/2)
Therefore, the coordinates of the midpoint between X and Y is (6, 11/2).
How to Find Midpoint?
Further, based on the points and their coordinate values, the following two midpoint methods are used to find the midpoint of the line segment joining the two points.
Method 1: If the line segment is vertical or horizontal, then dividing the length by 2 and counting that value from any of the endpoints will get us the midpoint of the line segment. Look at the figure shown below. The coordinates of points A and B are (-3, 2) and (1, 2) respectively. The length of the horizontal line \(\overline{AB}\) is 4 units. Half of this length is 2 units. Moving 2 units from the point (-3, 2) will give (-1, 2). So, (-1, 2) is the midpoint of \(\overline{AB}\).

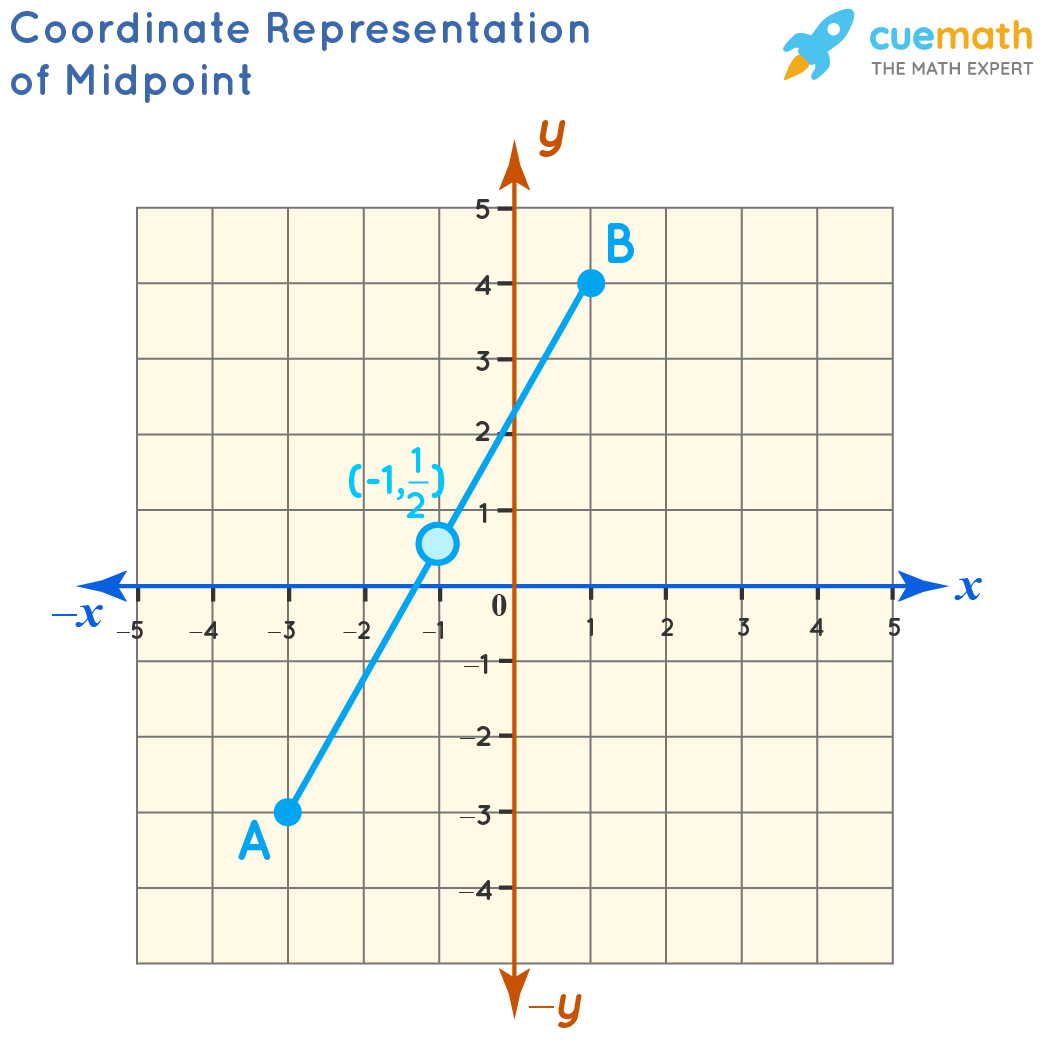
Method 2: The other way to find the midpoint is by using the midpoint formula. The coordinates of points A and B are (-3, -3) and (1, 4) respectively. Using midpoint formula, we have: ({-3 + 1}/2, {-3 + 4}/2) = (-2/2, 1/2)= (-1,1/2).
Method 3: One way to find the midpoint of a line given in a plane is by using construction. We can use a compass and straightedge construction to first construct a lens using circular arcs of equal (and large enough) radii centered at the two endpoints, then connecting the cusps of the lens (the two points where the arcs intersect). The point of intersection of the line connecting the cusps and the segment is the midpoint of the segment.
Here's an example to find the coordinate of an endpoint, given the midpoint and the coordinates of the other endpoint.
Example: Midpoint R between the points P and Q has the coordinates (4, 6). If the coordinates of Q are (8, 10), then what are the coordinates for point P? Solve it by using the midpoint formula.
Solution:
Let x coordinate of P be m and y coordinate of P be n.
P = (m, n)
Q = (8, 10)
R = (4, 6)
By using the midpoint formula,
R = ((m + 8)/2, (n + 10)/2) = (4, 6)
Solving for m,
(m + 8)/2 = 4
m + 8 = 8
m = 0
Solving for n,
(n + 10)/2 = 6
n + 10 = 12
n = 2
Therefore, coordinates of P are (0, 2).
Formulas Related to Midpoint
The midpoint formula includes computations separately for the x-coordinate of the points, and the y-coordinate of the points. The following two formulas are closely related to the midpoint formula.
Centroid of a Triangle Formula
The point of intersection of the medians of a triangle is called the centroid of the triangle. The median is a line joining the vertex to the midpoint of the opposite side of the triangle. The centroid divides the median of the triangle in the ratio 2:1. For a triangle with vertices (x1, y1), (x2, y2), (x3, y3) the formula to find the coordinates of the centroid of the triangle is as follows.
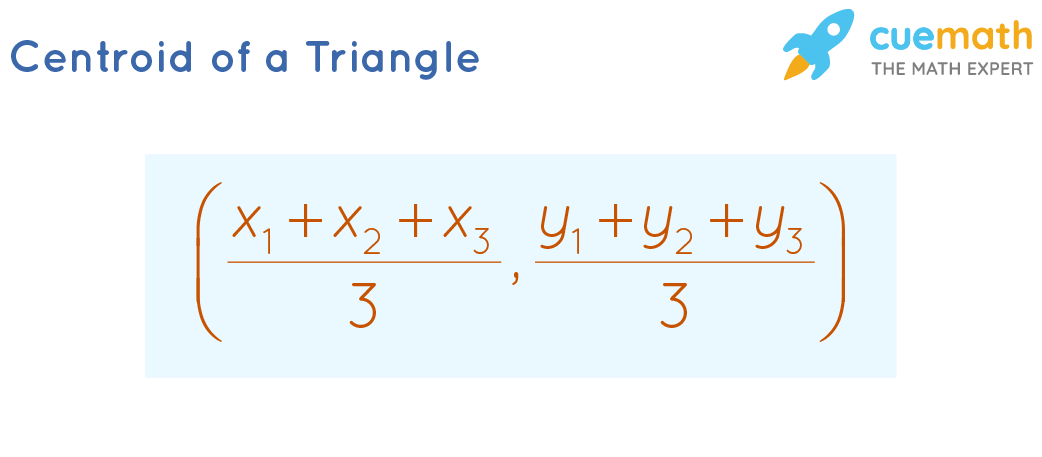
Section Formula
The section formula is helpful to find the coordinates of any point which is on the line joining the two points. Further, the ratio in which the point divided the line joining the two given points is needed to know the coordinates of the point. The point can be located between the points, or anywhere beyond the points, but on the same line. The section formula to find the coordinates of a point, which divides the line joining the points (x1, y1), and (x2, y2) in the ratio m:n is as follows. Here:
- The positive sign is used in the formula to find the coordinates of the point, which divides the points internally, and
- the negative sign is used if the point is dividing externally.

Important Notes on Midpoint:
The following points are the important properties of the midpoints.
- The midpoint divides a line segment in an equal ratio, that is, 1:1.
- The midpoint divides a line segment into two equal parts.
- The bisector of a line segment cuts it at its midpoint.
☛ Related Topics:
Midpoint Formula Examples
-
Example 1: The diameter of a circle has endpoints, (2, -3) and (-6, 5). Find the coordinates of the center of the circle.

Solution:
The center of a circle divides the diameter into 2 equal parts. So, it is a midpoint of the diameter. Let x1 = 2, y1 = -3, x2 = -6, and y2 = 5 The coordinates of the center is calculated as: ((x1 + x2)/2, (y1 + y2)/2) = ((2 + (-6))/2, (-3 + 5)/2) = (-4/2, 2/2) = (-2, 1).
Answer: ∴ the center of the circle is (-2, 1).
-
Example 2: Consider the line segment \(\overline{AB}\) shown below.

The endpoints are (1, h) and (5, 7). Find the value of h if the midpoint of \(\overline{AB}\) is (3, -2).
Solution:
Let x1 = 1, y1 = h, x2 = 5, and y2 = 7. According to the definition of midpoint we have, ((x1 + x2)/2, (y1 + y2)/2) = ((1 + 5)/2, (h + 7)/2) = (6/2, (h + 7)/2) = (3, (h + 7)/2). Equalizing this with the midpoint value (3, -2) we have (h + 7)/2 = -2; h + 7 = -2 × 2; h + 7 = -4; h = -4 - 7; h = -11.
Answer: ∴ the value of h is -11.
-
Example 3: The endpoints of a line segment are (2, h) and (4, 7). Find the value of h if the midpoint is (3, -1).
Solution:
Let x1 = 2, y1 = h, x2 = 4, and y2 = 7.
According to the definition of midpoint we have, ((x1 + x2)/2, (y1 + y2)/2) = ((2 + 4)/2, (h + 7)/2) = (6/2, (h + 7)/2) = (3, (h + 7)/2).
Equalizing this with the midpoint value (3, -1) we have (h + 7)/2 = -1;
h + 7 = -1 × 2
h + 7 = -2
h = -2 - 7; h = -9.
Therefore, the value of h is -9.
Answer: ∴ The value of h is -9.

FAQs on Midpoint Formula
What is the Midpoint Formula in Coordinate Geometry?
The midpoint formula in coordinate geometry is defined as the formula to find the center point of a straight line, using the coordinates of its endpoints. It says the midpoint of a line segment with coordinates (x1 y1) and (x2, y2) is given by the formula ((x1 + x2)/2, (y1 + y2)/2).
How to Use Midpoint Formula?
The midpoint formula is really simple when it comes to its applicability.
- Step 1: Identify the line segment or the two endpoints.
- Step 2: Find their coordinates.
- Step 3: Add the x coordinates of both the endpoints and divide by 2.
- Step 4: Add the y coordinates of both endpoints and divide by 2.
- Step 5: Write the values so obtained in steps 3 and step 4 as you mention the coordinates of any point.
☛ Also Check: You can try this midpoint calculator to verify the result obtained for the midpoint of a line segment- Midpoint Calculator
What is Meant by Midpoint?
A midpoint is defined as the point that is in the middle of the line joining two points. It is the point that is equidistant from both endpoints, thus bisecting the line segment.
What is the Midpoint Formula in Words?
For the midpoint of the line joining two points, whose coordinates are given, the midpoint formula in words can be described as the average of the x-coordinates of the two points and the average of the y-coordinates of the two points.
Can Midpoint be a Fraction?
Yes, the midpoint value can also be a fraction. It is basically dependent on the numeric value of the two points. The midpoint is the sum of the numeric value of two points, divided by 2. For points such as -4 and 5 on the number line, the midpoint is +1/2.
Why is the Midpoint Formula Important?
Midpoint formula has varied applications in real life, such as constructions purpose, etc. It has importance in geometry, such as
- Finding the coordinates of the centroid of a triangle.
- Finding the median of a triangle.
- Finding the midpoint of a line segment.
How do you Calculate Midpoint?
The midpoint can be found with the formula ((x1 + x2)/2, (y1 + y2)/2). Here (x1, y1), and (x2, y2) are the coordinates of two points, and the midpoint is a point lying equidistant and between these two points.
Can the Midpoint be Zero?
The midpoint can be zero. This is dependent on the value of the two points. For two points on a number line with values -4, and 4, the midpoint is 0; And for two points such as (-2, 5), and (2, -5), the midpoint is equal to (0, 0).
What is the Midpoint of a Curve?
The midpoint of a curve is the midpoint of the largest chord which can be drawn for the curve. The midpoint of a circle is the midpoint of its largest chord, which is the diameter of the circle.
What is the Midpoint of a Line?
The midpoint of a line is a point that is equidistant from the endpoints of the line and in the middle of the line. If the endpoints of the line are (x1, y1), and (x2, y2), then the formula for the midpoint of the line is ((x1 + x2)/2, (y1 + y2)/2).
What is the Midpoint of a Circle?
The midpoint of a circle is the center of the circle. The largest chord of the circle is the diameter, and the midpoint of the diameter of the circle is the midpoint of the circle. The midpoint of the circle is equidistant from every point on the circle.
What is the Midpoint of a Triangle?
The midpoint of the triangle is the centroid of the triangle. The centroid is the point of intersection of the medians of a triangle. The center of gravity of any triangular-shaped object is at its centroid.
visual curriculum