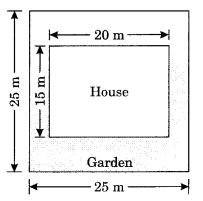
Mrs. Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ₹ 55 per m².
Solution:
The plot is square from the outside while the area of the house to be constructed is rectangular in the middle of the plot. From the diagram, we can see that the area of the garden is the difference between the area of the square plot and the area of the house.
Area of the square plot = side × side = 25 m × 25 m = 625 m²
Area of the house = length × breadth = 15 m × 20 m = 300 m²
Area of the garden to be developed = (Area of the square plot) - (Area of the house) = 625 m² - 300 m² = 325 m²
Hence, Area of the garden to be developed = 325 m²
The cost of developing a garden around the house = Rs 55 per m²
Therefore, the total cost of developing a garden of area 325 m² = 325 × 55 = Rs 17,875
☛ Check: NCERT Solutions for Class 8 Maths Chapter 11
Video Solution:
Mrs. Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ₹ 55 per m².
Class 8 Maths NCERT Solutions Chapter 11 Exercise 11.1 Question 2
Summary:
Mrs. Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. The total cost of developing a garden around the house at the rate of ₹ 55 per m² is ₹ 17,875.
☛ Related Questions:
- A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
- The shape of a garden is rectangular in the middle and semi circular at the ends as shown in the diagram. Find the area and the perimeter of this garden [Length of rectangle is 20 - (3.5 + 3.5) meters].
- A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m²? (If required you can split the tiles in whatever way you want to fill up the corners).
- An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, the circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle.
visual curriculum