Divisibility Rules
Divisibility rules are rules that are applied to a number to check whether the given number is divisible by a particular number or not. These divisibility tests help us skip the process of long division and help us mentally check if a number is completely divisible by another number. Let us learn more about the divisibility test and the divisibility rules with examples in this article.
| 1. | What are Divisibility Rules? |
| 2. | Divisibility Rules 2 to 12 |
| 3. | Divisibility Rules for Prime Numbers |
| 4. | FAQs on Divisibility Rules |
What are Divisibility Rules?
A divisibility rule is a kind of shortcut that helps us to identify if a given number is divisible by a divisor by examining its digits, without performing the long division process. These divisibility rules help us determine the actual divisor of a number just by considering the digits of that number. These are also called divisibility tests which help in larger calculations and ease out the process of simplification of numbers.
Divisibility Rules 2 to 12
In this section, let us learn about basic divisibility tests from 2 to 12. The divisibility rule of 1 is not required since every number is divisible by 1.
| Divisibility by number | Divisibility Rule |
|---|---|
| Divisible by 2 | A number that is even or a number whose last digit is an even number, i.e., 0, 2, 4, 6, and 8. |
| Divisible by 3 | The sum of all the digits of the number should be divisible by 3. |
| Divisible by 4 | The number formed by the last two digits of the number should be divisible by 4 or should be 00. |
| Divisible by 5 | Numbers having 0 or 5 as their ones place digit. |
| Divisible by 6 | A number that is divisible by both 2 and 3. |
| Divisible by 7 | Subtracting twice the last digit of the number from the remaining digits gives a multiple of 7. |
| Divisible by 8 | The number formed by the last three digits of the number should be divisible by 8 or should be 000. |
| Divisible by 9 | The sum of all the digits of the number should be divisible by 9. |
| Divisible by 10 | Any number whose ones place digit is 0. |
| Divisible by 11 | The difference of the sums of the alternative digits of a number is divisible by 11. |
| Divisible by 12 | A number that is divisible by both 3 and 4. |
Divisibility Rules Chart and Examples
Let us try to understand the above divisibility tests with examples.
- Is 280 divisible by 2? Yes, 280 is divisible by 2 as the units place digit is 0.
- Is 345 divisible by 3? Yes, 345 is divisible by 3, as the sum of all the digits, i.e., 3 + 4 + 5 = 12, and 12 is divisible by 3. So, 345 is divisible by 3.
- Is 450 divisible by 4? No, 450 is not divisible by 4 as the number formed by the last two digits starting from the right, i.e., 50 is not divisible by 4.
- Is 3900 divisible by 5? Yes, 3900 is divisible by 5 as the digit at the units place is 0 which satisfies the divisibility rule of 5.
- Is 350 divisible by 6? The sum of all the digits of 350 is 8, so it is not divisible by 3. Hence it cannot be divisible by 6, as a number needs to be a common multiple of both 2 and 3 to be a multiple of 6.
- 357 is divisible by 7 as when we subtract the twice of the ones place digit, 7 × 2 = 14, and subtract it from the remaining digits 35, we get 35 -14 = 21, which is divisible by 7. So, 357 is divisible by 7.
- 79238 is not divisible by 8, as the number formed by the last three digits 238 is not completely divisible by 8.
- 875 is not divisible by 9, as the sum of all the digits, 8 + 7 + 5 = 20 is not divisible by 9.
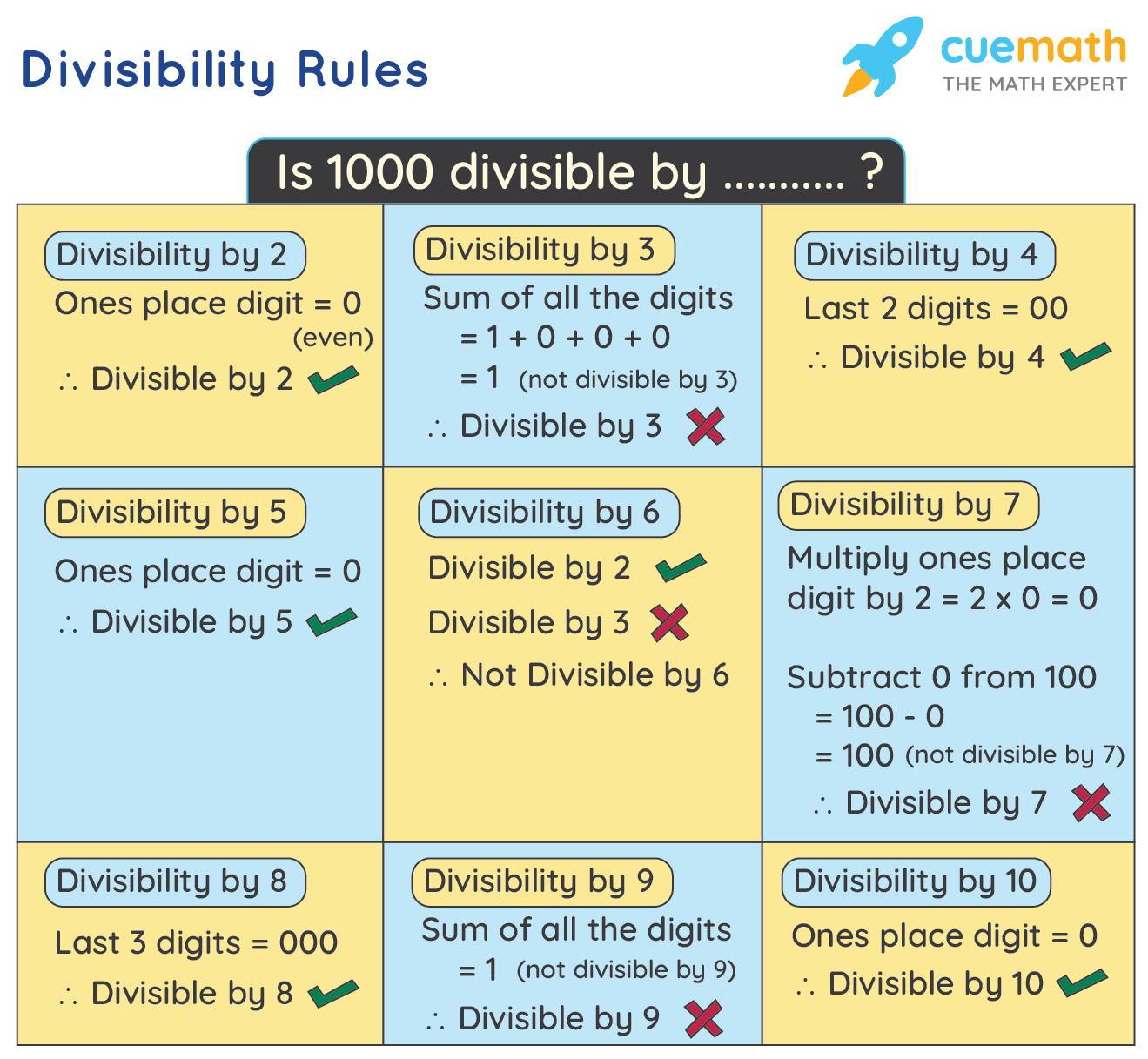
Now, let us take the number 1000 and see its divisibility by 2 to 10. It is clearly seen in the following figure that 1000 is divisible by 2, 4, 5, 8, and 10, and not divisible by 3, 6, 7, and 9. We find this by applying the divisibility rules of 2 to 10, and not by performing division which can be more time-consuming.
Divisibility Rules for Prime Numbers
Intermediate divisibility rules are applied to prime numbers which are less than 20 and greater than 10. Divisibility tests for prime numbers 2, 3, 5, 7, and 11 are already discussed above. Here, let's learn about the divisibility rules of 13, 17, and 19.
Divisibility Rule of 13 - A number is divisible by 13 if it leaves 0 as the remainder when we divide it by 13. The divisibility test of 13 helps us quickly know if a number is divisible by 13 or not without performing long division. According to the divisibility rule of 13, first, we need to multiply the ones place digit by 4. Then, we add the product to the rest of the number to its left (excluding the digit at the units place). If that sum results in a number divisible by 13, then the original number is also divisible by 13. Apart from this method, there are three other divisibility rules of 13 that are explained in this article - Divisibility Rule of 13.
Divisibility Rule of 17 - A number is divisible by 17 when 17 divides it completely without leaving any non-zero remainder. According to the divisibility rule of 17, first, we need to multiply the ones place digit by 5. Then, we subtract the product from the rest of the number to its left (excluding the digit at the units place). If that difference results in a number divisible by 17, then the original number is also divisible by 17.
Divisibility Rule of 19 - If we get 0 as the remainder when dividing a number by 19, then that number is considered divisible by 19. According to the divisibility rule of 19, first, we need to multiply the ones place digit by 2. Then, we add the product to the rest of the number to its left (excluding the digit at the units place). If that sum results in a number divisible by 19, then the original number is also divisible by 19.
Divisibility Rules of 13, 17, and 19 Examples
Let us take the example of number 1326, and check its divisibility by 13, 17, and 19. Observe the figure given below to understand this example.

- Divisibility rules are of great importance while checking prime numbers.
- These are handy to solve word problems.
- They are useful to do quick calculations.
- Every even number is divisible by 2.
- Every leap year is divisible by 4.
Divisibility Tests of Numbers
Also, check these articles related to the divisibility rules.
Divisibility Rules with Examples
-
Example 1: Test the divisibility of the following numbers by 2.
236, 254, 289, 278
Solution:
As per the divisibility rule of 2, a number is divisible by 2 if it is even or if the last digit is an even number, i.e., 2, 4, 6, 8 including 0.
So, let us apply this rule to all the given numbers.
a.) 236: Here, the last digit is 6 which is an even number. Therefore, 236 is divisible by 2.
b.) 254: Here, the last digit is 4 which is an even number. Therefore, 254 is divisible by 2.
c.) 289: Here, the last digit is 9 which is an odd number. Therefore, 289 is not divisible by 2.
d.) 278: Here, the last digit is 8 which is an even number. Therefore, 278 is divisible by 2.
Thus, out of the listed numbers, 236, 254, 289, and 278, only 289 is not divisible by 2. This means 236, 254, and 278 are divisible by 2.
-
Example 2: Check the divisibility of the following numbers by 9:
354, 765, 243, 405
Solution:
As per the divisibility rule of 9, the sum of all the digits of the number should be divisible by 9. So, let us apply this rule to all the given numbers:
a.) 354: Here, 3 + 5 + 4 = 12, but 12 is not divisible by 9. Therefore, 354 is not divisible by 9.
b.) 765: Here, 7 + 6 + 5 = 18 and 18 is divisible by 9. Therefore, 765 is divisible by 9.
c.) 243: Here, 2 + 4 + 3 = 9, and 9 is divisible by 9. Therefore, 243 is divisible by 9.
d.) 405: Here, 4 + 0 + 5 = 9 and 9 is divisible by 9. Therefore, 405 is divisible by 9.
Thus, out of the listed numbers, 354, 765, 243, and 405 only 354 is not divisible by 9. This means 765, 243, and 405 are divisible by 9.
-
Example 3: Test the divisibility of the following numbers by 3:
18657, 967458, 263705
a.) 18657: Here, 1 + 8 + 6 + 5 + 7 = 27 and 27 is divisible by 3. Therefore, 18657 is divisible by 3.
b.) 967458: Here, 9 + 6 + 7 + 4 + 5 + 8 = 39 and 39 is divisible by 3. Therefore, 967458 is divisible by 3.
c.) 263705: Here, 2 + 6 + 3 + 7 + 0 + 5 = 23 and 23 is not divisible by 3. Therefore, 263705 is not divisible by 3.
Thus, out of the listed numbers 18657, 967458, and 263705, the number 263705 is not divisible by 3. This means 18657 and 967458 are divisible by 3.

FAQs on Divisibility Rules
What are Divisibility Rules?
Divisibility rules are those rules which help us identify whether a number is completely divisible by another number or not. Divisibility tests are short calculations based on the digits of the numbers to find out if a particular number is dividing another number completely or not.
What is the Divisibility Rule of 7 and 11?
The divisibility rule of 7 states that if we multiply the units place digit of the number by 2, and then if the difference between that number and the rest of the number to the left is divisible by 7, then the number is also divisible by 7. For example, let us check whether the number 3437 is divisible by 7 or not.
- First, multiply the units place digit of 3437 by 2, i.e., 7 × 2 =14.
- Now, subtract 14 from the rest of the number on the left, which is 343. So, 343 - 14 = 329. It is still difficult to figure out whether 329 is divisible by 7 or not, so we will repeat the same process again.
- Multiply the units place digit of 329 by 2, i.e., 9 × 2 =18. After we subtract 18 from 32, we get 32 - 18 =14, which is divisible by 7. So, 3437 is divisible by 7.
The divisibility rule of 11 states that if the difference between the sums of the digits at the alternative places of a number is divisible by 11, then the number is also divisible by 11.
- To check if 1334 is divisible by 11 or not, find the sum of the digits at the alternative places first.
- The sum of the digits at the odd places is 4 + 3 = 7 and the sum of the digits at the even places is 3 + 1 = 4.
- Now find the difference between the two, which is 7 - 4 = 3. And we know that 3 is not divisible by 11, so 1334 is also not divisible by 11.
What are the Divisibility Rules for 2, 5, and 10?
The divisibility rules of 2, 5, and 10 are given below:
- Divisibility rule of 2 - The units place digit of the number should be either 0, 2, 4, 6, or 8.
- Divisibility rule of 5 - The units place digit of the number should be either 0 or 5.
- Divisibility rule of 10 - The units place digit of the number should be 0.
What are the Divisibility Rules for 3, 6, and 9?
The divisibility rules of 3, 6, and 9 are given below:
- Divisibility rule of 3 - The sum of all the digits of the number should be divisible by 3.
- Divisibility rule of 6 - The number should be divisible by both 2 and 3.
- Divisibility rule of 9 - The sum of all the digits of the number should be divisible by 9.
What are the Divisibility Rules for 8?
To check whether a number is divisible by 8 or not, we can use the divisibility test of 8 which states that for a number to be divisible by 8 either of the following should be true:
- The last three places of the number from the right should be 000.
- The last three places of the number should be a number divisible by 8.
What is the Divisibility Test of 7?
The following steps are used to check the divisibility test of 7:
- Step 1: Identify the ones place digit of the number and multiply it by 2.
- Step 2: Find the difference between the number obtained in step 1 and the rest of the number.
- Step 3: If the difference is divisible by 7, then the number is divisible by 7.
- Step 4: If it is still difficult to identify whether the difference is a multiple of 7 or not, repeat the same process with the number obtained in step 2.
What is the Divisibility Test of 2?
The divisibility test of 2 states that if the ones place digit of a number is even including 0, then the number will be divisible by 2. All the even numbers are divisible by 2. It is to be noted that these numbers are multiples of 2.
What is the Use of Divisibility Rules?
In math, divisibility tests are important to learn as it helps us to ease out our calculations in multiplication and division. We can quickly identify whether a particular number is divisible by another number or not by applying divisibility rules.
How many Divisibility Rules are there?
Generally, we have divisibility rules from 1 to 20. But if we are able to identify the pattern of multiples of numbers, we can create more divisibility tests. For example, the divisibility rule of 21 states that a number must be divisible by both 3 and 7. It is because 21 is a multiple of two prime numbers 3 and 7, so all the multiples of 21 will definitely have 3 and 7 as their common factors.
visual curriculum