A day full of math games & activities. Find one near you.

Resultant Vector Formula

Resultant vector formula is used to obtain the resultant value of two or more vectors. This is obtained by computing the vectors based on the directions with respect to each other. Resultant vector formula has numerous applications in physics, engineering. An example of this is the interplay of numerous force vectors on a body, where this formula is used to obtain the resultant vector.

What is the Resultant Vector Formula?

The resultant vector formula is of three kinds based on the direction of the vectors. These formulas are for vectors in the same direction, for vectors in the opposite direction, and for vectors inclined to each other.

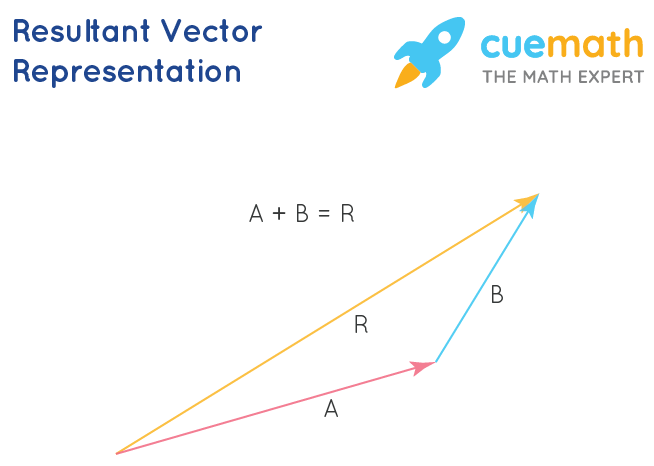
Formula 1 Vectors in the same direction can be simply added to obtain the resultant vector. Here A, B are the vectors in the same direction and R is the resultant vector.

R = A + B

Formula 2 Vectors in the opposite direction are subtracted from each other to obtain the resultant vector. Here the vector B is opposite in direction to the vector A, and R is the resultant vector.

R = A - B

Formula 3 Vectors inclined to each other are computed with the below formula to obtain the resultant vector. Hre the vectors A and B are inclined at an angle Ø to each other, and R is the resultant vector.

R² = A² + B² + 2ABCosØ

Resultant Vector Representation

Breakdown tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

Solved Examples on Resultant Vector Formula

Example 1: Find the resultant of the vectors 4i + 3j -5k and 8i + 6j - 10k.

Solution:

The given two vectors are:
A = 4i + 3j - 5k and B = 8i + 6j - 10k
The direction ratios of the two vectors are in equal proportion and hence the two vectors are in the same direction.
The following resultant vector formula can be used here.
R = A + B
= (4i + 3j - 5k) + (8i + 6j - 10k)
= 12i + 9j - 15k

Answer: Hence the resultant of the two vectors is 12i + 9j - 15k.
Example 2: Find the resultant of the vectors having magnitudes of 5 units, 6 units, and are inclined to each other at an angle of 60 degrees.

Solution:

The two vectors are A = 5 units, B = 6 units and the angle Ø = 60°.
The resultant vector can be obtained by the following formula.
R² = A² + B²+ 2ABCosØ
= 5² + 6²+ 2×5×6×Cos60°
= 25 + 36 + 60 × 1/2
= 61 + 30
R² = 91
R = √91

Answer: Therefore the resultant vector is √91.

go to slide go to slide