Sin Squared x Formula
Sin squared x means sin x whole squared. There is two sin squared x formulas. One of them is derived from one of the Pythagorean identities and the other is derived from the double angle formula of the cosine function. The former is used in proving various trigonometric identities whereas the latter is widely used in solving the integrals. Let us learn the sin squared x formulas along with derivations and a few solved examples.

What Are Sin Squared x Formulas?
Using one of the trigonometric identities, we have sin2x + cos2x = 1. Subtracting cos2x from both sides, we get sin2x = 1 - cos2x. Thus, one of the sin squared x formulas is,
\(\sin^2x = 1-\cos^2x\)
Using one of the double angle formulas of cosine function, we have cos 2x = 1 - 2 sin2x. If we solve this for sin2x, we get:
\(\sin^2x = \dfrac{1-\cos 2x}{2} \)
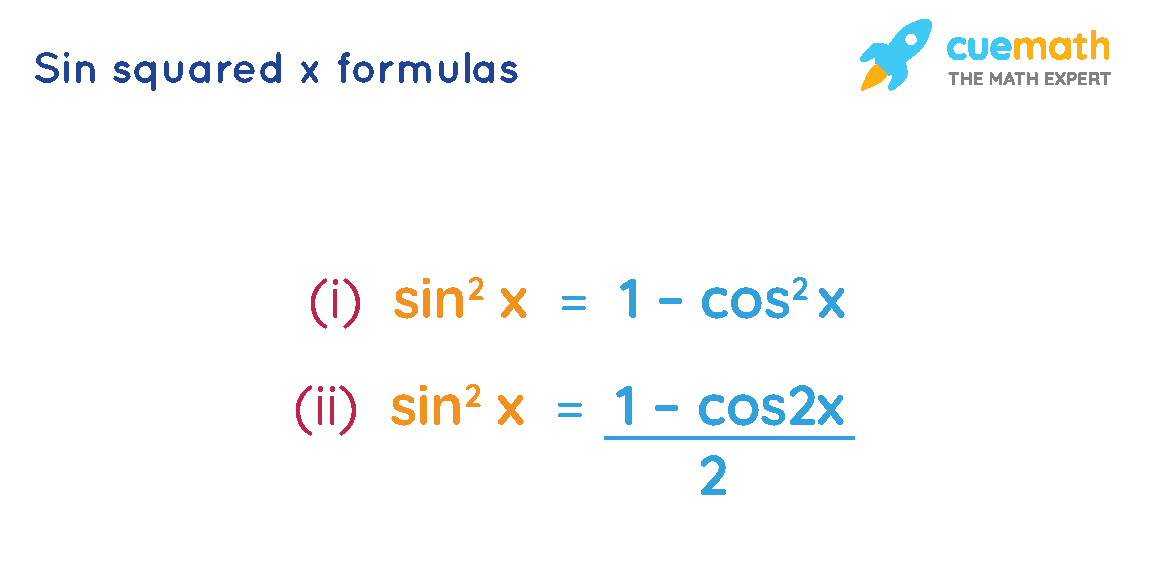
Let us see the usage of the sin squared x formulas in the following solved examples.
Solved Examples Using Sin Squared x Formulas
-
Example 1: Prove the following trigonometric identity using the sin squared x formula: sin2x - sin4x = cos2x - cos4x.
Solution:
We will use the sin squared x formula, sin2x = 1 - cos2x to prove this.
\( \begin{align} \sin^2x - \sin^4x&= \sin^2x (1- \sin^2x)\\[0.2cm] &= \sin^2x \cos^2x \\[0.2cm] &= (1-\cos^2x) \cos^2x \\[0.2cm] &= \cos^2x -\cos^4x \end{align}\)
Answer: The given identity is proved.
-
Example 2: Find the value of \(\int \sin^2x \,dx\).
Solution:
By one of the sin squared x formulas, \(\sin^2x = \dfrac{1-\cos 2x}{2} \). So
\( \begin{align}&\int \sin^2x \, dx\\[0.2cm] &= \int \left( \dfrac{1- \cos 2x}{2}\right)dx \\[0.2cm] &= \dfrac{1}{2} \int(1-\cos 2x) dx\\[0.2cm] &= \dfrac{1}{2} \left(x - \dfrac{\sin 2x}{2} \right)+C\\[0.2cm] &= \dfrac{x}{2} - \dfrac{\sin 2x}{4} + C \end{align}\)
Answer: \(\int \sin^2x \,dx = \dfrac{x}{2} - \dfrac{\sin 2x}{4} + C\).
visual curriculum