Prove That Root 6 is Irrational Number
Is root 6 an irrational number? Mathematically, a number that is represented in p/q form where p and q both are integers, and q is not equal to 0, is referred to as a rational number whereas the number that cannot be represented in p/q form are called irrational numbers. A number whose decimal expansion keeps extending after the decimal point is also categorized as an irrational number. Now let us take a look at the detailed discussion and prove that root 6 is irrational.
Prove That Root 6 is Irrational Number
Problem statement: Prove that root 6 is an irrational number
Proof: When we calculate the value of √6, we get √6 = 2.449489742783178... It is a decimal number that does not terminate and terms are not repeating themselves after the decimal point. Thus, the value obtained for the root of 6 satisfies the condition of being a non-terminating and non-repeating decimal number that keeps extending further after the decimal point which makes √6 an irrational number.
Hence, √6 is an irrational number.
Root 6 is most commonly used to term square root of 6. We represent the root of a number "n" as √n. Thus, the root of a number is defined as the number that on squaring gives the original number. For example, squaring √6, we get the number 6. In order to prove that root 6 is an irrational number, we can use two different methods. They are:
- Contradiction method
- Long division method
Let's move further and discuss both the methods in detail.
Prove That Root 6 is Irrational by Contradiction Method
Given: Number √6
To Prove: Root 6 is irrational
Proof: Let us assume that square root 6 is rational. As we know a rational number can be expressed in p/q form, thus, we write, √6 = p/q, where p, q are the integers, and q is not equal to 0. The integers p and q are coprime numbers thus, HCF (p,q) = 1.
√6 = p/q
⇒ p = √6 q ------- (1)
On squaring both sides we get,
⇒ p2 = 6 q2
⇒ p2/6 = q2 ------- (2)
If k was a prime number and k divides a2 evenly, then k also divides 'a' evenly, where a is any positive integer.
Hence the equation (2) shows 6 is a factor of p2 which implies that 6 is a factor of p.
We can write p = 6b (where b is a constant)
Substituting p = 6b in (2), we get
(6b)2/6 = q2
⇒ 36b2/6 = q2
⇒ 6b2 = q2
⇒ b2 = q2/6 ------- (3)
Hence, similarly, equation (3) shows that 6 is a factor of q
We can see from equations (2) and (3) that 6 is a factor of p and 6 is a factor of q respectively which contradicts our assumption that p and q are coprime numbers. Therefore we can conclude that our assumption of taking root 6 as a rational number was wrong.
Thus, the square root of 6 is irrational.
Prove That Root 6 is Irrational by Long Division Method
We can obtain the value of the root 6 by the long division method using the following steps:
- Step 1: First the number 6 is written as 6.00 00 00 and the digits are paired starting from one's place.
- Step 2: Now we find a number whose square results in a number equal to or less than 6.
- Step 3: The quotient is 2 and the remainder obtained is 2.
- Step 4: Bring down the first pair of zeros. Now, 200 becomes the new dividend.
- Step 5: Double the quotient obtained. It is 2 and now the new divisor will be 2n which when multiplied by n should get the product less than or equal to 200.
- Step 6: We determine 44 × 4 = 176. On subtracting this from 200 we get the remainder as 24. Bring down the next pair of zeros. 2400 becomes the new dividend.
- Step 7: Add the unit place digit in the divisor, we get 44+4. It is 48 and now let us have our new divisor, 48n.
- Step 8: Find a digit 'n' such that 48n × n gives the product less than or equal to 2400. We determine 484 × 4 = 1936. On subtracting this from 2400 the remainder obtained is 464. Bring down the next pair of zeros. 46400 becomes the new dividend.
- Step 9: Add the unit place digit in the divisor, we get 484+4. It is 488 and now let us have our new divisor, 488n. Find a digit 'n' such that 488n × n gives the product less than or equal to 46400. We determine 4889 × 9 = 44001. On subtracting this from 46400 the remainder obtained is 2399.
- Step 10: The long division is continued until the required number of digits after the decimal is obtained.
As we can see the value of root 6 does not terminate after 3 decimal places. It can still be extended further. Hence, this makes √6 an irrational number.
☛ Also Check:
- Prove that Root 2 is Irrational
- Prove that Root 3 is Irrational
- Prove that Root 5 is Irrational
- Prove that Root 7 is Irrational
- Prove that Root 11 is Irrational
Solved Examples
-
Example 2: Jenny said to her friend Lisa that the square root of 6 is an irrational number. She then asked her to find √6 using a number line. Can you help her?
Solution: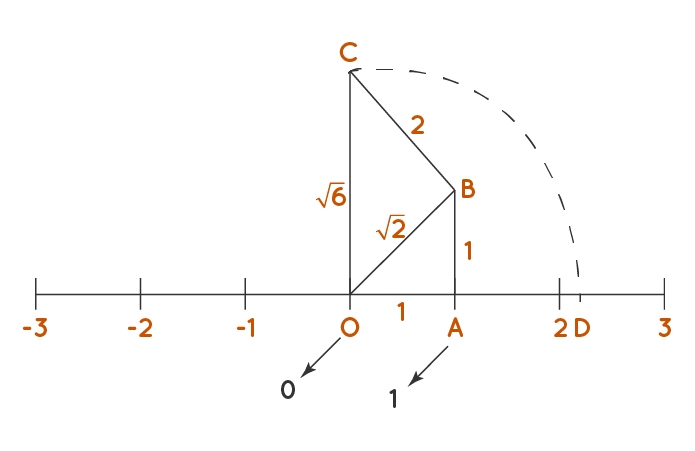
Following are the steps to construct the root 6 on the number line.
- Step 1: First draw OA = 1 unit on the number line, and by drawing a perpendicular line AB from A, where AB = 1 unit, join OB.
- Step 2: We can conclude that the line segment OB will measure √2 by using the Pythagorean Theorem as OB = √(OA2 + AB2) = √(12 + 12) = √2 units.
- Step 3: Draw a perpendicular line BC from B, where CB = 2 unit, join OC.
- Step 4: Now applying the Pythagorean theorem, we get OC = √(OB2 + BC2) = √((√2)2 + 22) = √6 units.
- Step 5: Now make an arc meeting on the number line considering OC as the radius which represents √6 units.
- Step 6: Thus, OC and OD measure √6 units respectively.
Thus, √6 is represented on the number line.
FAQs on Is Root 6 an Irrational?
How Do You Prove That Root 6 is Irrational?
We can prove that root 6 is an irrational number by different methods. We cannot express root 6 in p/q form where p, q are integers and q is not equal to 0, which tells us that it is an irrational number. The value of the square root of 6 is √6 = 2.449489742783178... and it does not terminate and terms do not repeat as well, after the decimal but only extends further, which is a property of an irrational number. We can also prove that root 6 is irrational, one by using the method of contradiction and the other by using the method of long division.
Is 2 times the square root of 6 Irrational?
Yes, 2 times the square root of 6 is an irrational number. 2 times the square root 6 is written as 2 × √6 = 2 × 2.449489742783178 = 4.898979485566356... Here, we get a result that is a decimal number that does not terminate and whose terms do not repeat as well, hence it can be said that it is an irrational number. From this, it can be seen that any number multiplied with root 6 will be irrational.
How to Prove Root 6 is Irrational by Contradiction?
We can prove that root 6 is irrational using contradiction we use the following steps:
- Step 1: It is assumed that √6 is rational.
- Step 2: Now, we write √6 = p/q
- Step 3: On squaring both sides, the obtained equation is simplified and a constant value is substituted.
- Step 4: Hence, it is found that 6 is a factor of the numerator and the denominator which contradicts the property of a rational number.
hence, root 6 is an irrational number is proved.
Is 3 Times the Square Root of 6 Irrational?
Yes, 3 times the square root of 6 gives an irrational number. We write 3 times the square root 6 as 3 × √6 = 3 × 2.449489742783178 = 7.348469228349534... Here, we can see that any number multiplied with root 6 will be irrational. Therefore, 3 times the square root of 6 is irrational too.
How to Prove that 1 by Root 6 is irrational?
When we rationalize 1/√6, we get (1/√6) × (√6/√6) = √6/6. It is known to us that √6 is an irrational number, and dividing an irrational number by a rational number also gives an irrational number, this helps us conclude that 1/√6 is irrational.