Prove that Root 3 is Irrational Number
Is root 3 an irrational number? Numbers that can be represented as the ratio of two integers are known as rational numbers, whereas numbers that cannot be represented in the form of a ratio or otherwise, those numbers that could be written as a decimal with non-terminating and non-repeating digits after the decimal point are known as irrational numbers. The square root of 3 is irrational. It cannot be simplified further in its radical form and hence it is considered as a surd. Now let us take a look at the detailed discussion and prove that root 3 is irrational.
Prove that Root 3 is Irrational Number
The square root of a number is the number that when multiplied by itself gives the original number as the product. A rational number is defined as a number that can be expressed in the form of a division of two integers, i.e. p/q, where q is not equal to 0.
√3 = 1.7320508075688772... and it keeps extending. Since it does not terminate or repeat after the decimal point, √3 is an irrational number. We can learn to prove that root 3 is irrational by following different methods.
Prove That Root 3 is Irrational by Contradiction Method
There are many ways in which we can prove the root of 3 is irrational by contradiction. Let us get one such proof.
Given: Number 3
To Prove: Root 3 is irrational
Proof:
Let us assume the contrary that root 3 is rational. Then √3 = p/q, where p, q are the integers i.e., p, q ∈ Z and co-primes, i.e., GCD (p,q) = 1.
√3 = p/q
⇒ p = √3 q
By squaring both sides, we get,
p2 = 3q2
p2 / 3 = q2 ------- (1)
(1) shows that 3 is a factor of p. (Since we know that by theorem, if a is a prime number and if a divides p2, then a divides p, where a is a positive integer)
Here 3 is the prime number that divides p2, then 3 divides p and thus 3 is a factor of p.
Since 3 is a factor of p, we can write p = 3c (where c is a constant). Substituting p = 3c in (1), we get,
(3c)2 / 3 = q2
9c2/3 = q2
3c2 = q2
c2 = q2 /3 ------- (2)
Hence 3 is a factor of q (from 2)
Equation 1 shows 3 is a factor of p and Equation 2 shows that 3 is a factor of q. This is the contradiction to our assumption that p and q are co-primes. So, √3 is not a rational number. Therefore, the root of 3 is irrational.
Prove That Root 3 is Irrational by Long Division Method
The irrational numbers are non-terminating decimals and this can be proved in the case of root 3 as well. Divide 3 using the long division algorithm.
- Write 3 as 3 00 00 00. Consider the number in pairs from the right. So 3 stands alone.
- Now divide 3 with a number such that the number × number gives 3 or a number lesser than that. We determine 1 × 1 = 1
- Subtract this product from 3 and get the remainder as 2. Obtain 1 as the quotient. Bring down the first pair of zeros. 200 becomes the new dividend.
- Double the quotient obtained. It is 2 and now let us have our new divisor, 2n which when multiplied by n should get the product less than or equal to 200.
- We determine 27 × 7 = 189. Subtract this from 200 and get the remainder as 11. Bring down the next pair of zeros. 1100 becomes the new dividend.
- Double the quotient obtained. It is 34 and now let us have our new divisor, 34n. Find a digit 'n' such that 34n × n gives the product less than or equal to 1100.
- We determine 343 × 3 = 1029. Subtract this from 1100 and get the remainder as 71. Bring down the next pair of zeros. 7100 becomes the new dividend.
- Repeat the same division process until we get the quotient approximated to 3 decimal places. Thus, we have evaluated √3 = 1.732
- This is a never-ending process. We get non-terminating and non-repeating digits after the decimal point. √3 = 1.7320508075688772 and it goes on.
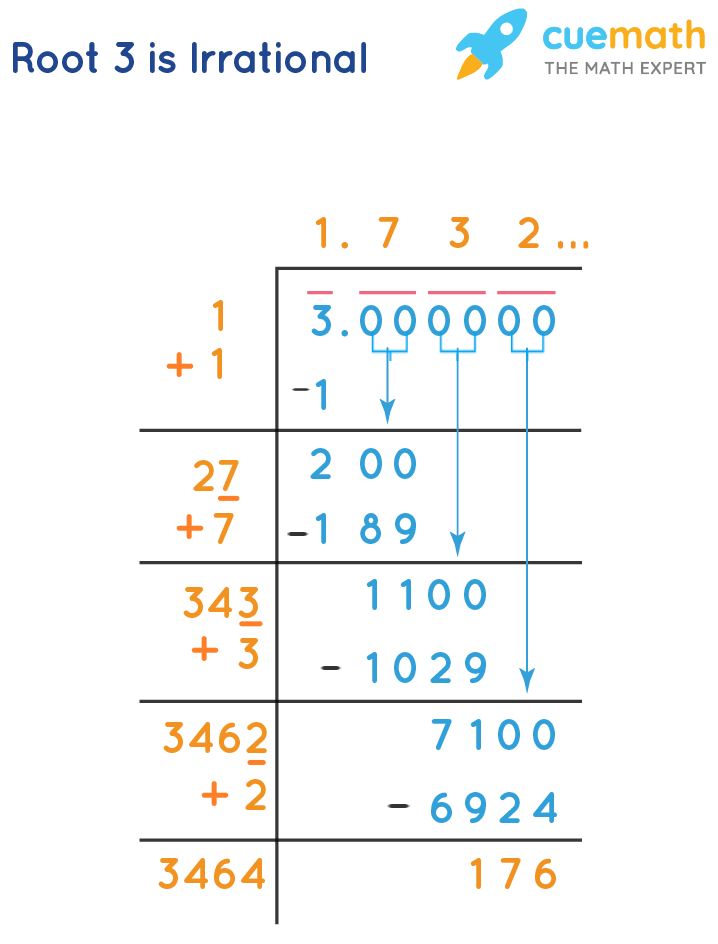
Also Check:
Solved Examples
-
Example 2: Peter said to his friend Frank that the square root of 3 is an irrational number. He then asked him to find √3 using a number line. Can you help him?
Solution:Look at the image below showing root 3 on the number line and read the explanation given below it to understand the process.
Let us construct root 2 on the number line. Draw the number line and number it as -1, 0, 1, and 2 at equal intervals of 1 unit each. Now consider OA = 1 unit on the number line. Construct a perpendicular line AB = 1 unit. Join OB. Applying the Pythagorean Theorem, we get (√(OA2 + AB2) = √(12 + 12) = √2
Thus OB = √2
We can conclude that the line segment OB = √2. Construct BC perpendicular to OB, and join OC. Applying the Pythagorean theorem, we get OB2 + BC2 = OC2
(√2)2 + (√1)2 = OC2
OC2 = 2 +1 = 3 ⇒ OC = √3
We can conclude that OC is the line that represents root 3. Now, with OC as the radius, and O as the center, construct an arc CD, such that the arc meets the number line at D.
OC = √3 = OD (same radius as OC)
Thus √3 is represented on the number line as OD.
FAQs on Is Root 3 an Irrational
How do you Prove that Root 3 is Irrational?
Root 3 is irrational is proved by the method of contradiction. If root 3 is a rational number, then it should be represented as a ratio of two integers. We can prove that we cannot represent root is as p/q and therefore it is an irrational number.
Is 2 times the square root of 3 Irrational?
Yes, 2√3 is irrational. 2 × √3 = 2 × 1.7320508075688772 = 3.464101615137754..... and the product is a non-terminating decimal. This shows 2√3 is irrational. The other way to prove this is by using a postulate which says that if we multiply any rational number with an irrational number, the product is always an irrational number. That is why 2√3 is irrational.
How to Prove Root 3 is Irrational by Contradiction?
Let us assume, to the contrary, that root 3 is rational. That is, we can find co primes p and q where q ≠ 0, such that √3 = p/q.
Rewriting, we get √3q = p. Squaring on both sides, we get the equation 3q2 = p2. Hence p2 is divisible by 3, and so p is also divisible by 3. Hence we can write p = 3c for some integer c. Substituting p = 3c in our equation, we get 3q2 = 9c2 ⇒ q2 =3c2 . This shows q is also divisible by 3. Thus p and q have at least 3 as a common factor. But this contradicts our assumption that p and q are co-primes. Therefore, our assumption was wrong, and root 3 is an irrational number.
Is 3 Times the Square Root of 3 Irrational?
Yes, 3√3 is irrational. 3 × √3 = 3 × 1.7320508075688772... = 5.196152422706631.......... and the product is a non-terminating decimal. This shows 3√3 is irrational. The other way to prove this is by using a postulate which says that if we multiply any rational number with an irrational number, the product is always an irrational number. That is why 3√3 is irrational.
How to Prove that 1 by Root 3 is irrational?
1 by root 3 can be rationalized as, \(\dfrac{1}{√3} \times \dfrac{√3}{√3} = \dfrac{√3}{3}\). Now, we know that the product of a rational and an irrational number is always irrational. Here, 1/3 is a rational number and √3 is an irrational number. Therefore, it is proved that 1 by Root 3 is irrational.