Prove that Root 7 is Irrational Number

Is root 7 an irrational number? A number that can be represented in p/q form where q is not equal to 0 is known as a rational number whereas numbers that cannot be represented in p/q form are known as irrational numbers. An irrational number can also be denoted as a number that does not terminate and keeps extending after the decimal point. Now that we know about rational and irrational numbers, let us look at the detailed discussion and prove that root 7 is an irrational number. 

The square root of 7 will be an irrational number if the square root of 7 gives a value after decimal that is non-terminating and non-repeating. Before going forward, let us discuss quickly, the root of the number "n". The square root of a number n is denoted by the symbol √n. As we multiply the root of a number to itself it gives the original number whose root we have taken. Therefore,  √7 on multiplication to itself gives the number 7.

We can prove that root 7 is an irrational number, with the help of various methods like the contradiction method and long division method.

It is known that a decimal number that has a value that does not terminate and does not repeat as well, then it is an irrational number. The value of √7 is 2.64575131106... It is clear that the value of root 7 is also non-terminating and non-repeating. This satisfies the condition of √7 being an irrational number. Hence, √7 is an irrational number. 

We can prove that root 7 is irrational also by using the contradiction method.

To prove: We want to prove that root 7 is irrational.
Proof: We will start with the contradictory statement of what we have to prove. Let us assume that square root 7 is rational.

Now since it is a rational number, it can be written in the form p/q, where p, q ∈ Z, and coprime numbers, i.e., GCD (p,q) = 1.

⇒ √7 = p/q
On rearranging the terms, we get
⇒ p = √7 q ------- (1)

On squaring both sides we get, 
⇒ p² = 7 q² 
Again rearranging the terms,
⇒ p²/7 = q² ------- (2)

As we know, 7 is a prime number. Using the theory, which says that, if a prime number k divides m², then it also divides m, and vice versa is also true. This implies that since 7 is a factor of p² then it will also be the factor of p.

Thus we can write p = 7a (where a is some constant)

Substituting p = 7a in equation (2), we get 
(7a)²/7 = q²
⇒ (49a²)/7 =  q² 
⇒ 7a²  =  q² 
Rearranging,
⇒ a²  =  q²/7 ------- (3)

This shows that 7 will also be the factor of q.
Now, initially, we have assumed that p and q are the coprime numbers hence only 1 is the number that can evenly divide both of them. But here, we have 7 is the common factor of p and q, which is contradictory to our initial assumption.

This proves that the assumption of root 7 as a rational number was incorrect. Therefore, the square root of 7 is irrational.

There is one more method by which we can prove that root of 7 is irrational and that is the long division method. We find out the value of the root 7 by long division method and check whether we get the non-terminating and non-repeating value after decimal or not.

The long division method can be applied using the following steps:

• Step 1: Add pairs of 0 after 7 as 7.00 00 00 and pair the digits starting from the right and find a number whose square is less than or equal to the number 7, it will be our first divisor and quotient. We have 2 square the number and subtract the result from 7, 3 is the remainder.
   
• Step 2: Take the next pair of 0 down after the remainder, as 00 is brought down, we get 300 as the next dividend, and double the first quotient to get the partial divisor of this step. The unit digit the divisor will be the number which on multiplying with the complete divisor thus formed, gives a number equal or less than the new dividend. Here, we get 6 at the units place, and 46 is our divisor and 6 is our quotient. Subtract the result after multiplying 46 with 6 from 300, and note down the remainder. 
   
• Step 3: Take the next pair of 0 down after the remainder of the previous step to get the dividend, 2400 is the new dividend. Add the units place of the divisor obtained in the previous step to the divisor itself and get the partial divisor of this step. Here, we get 52. The unit digit the divisor will be the number which on multiplying with the complete divisor thus formed, gives a number equal or less than the new dividend. Here, we get 4 at the units place, and 524 is our divisor and 4 is our new quotient. Subtract the result after multiplying 524 with 4 from 2400, and note down the remainder. 
   
• Step 4: Repeat the process until the required number of digits after the decimal is obtained.

See the following image to see a few of the steps in the long division of the 7. 

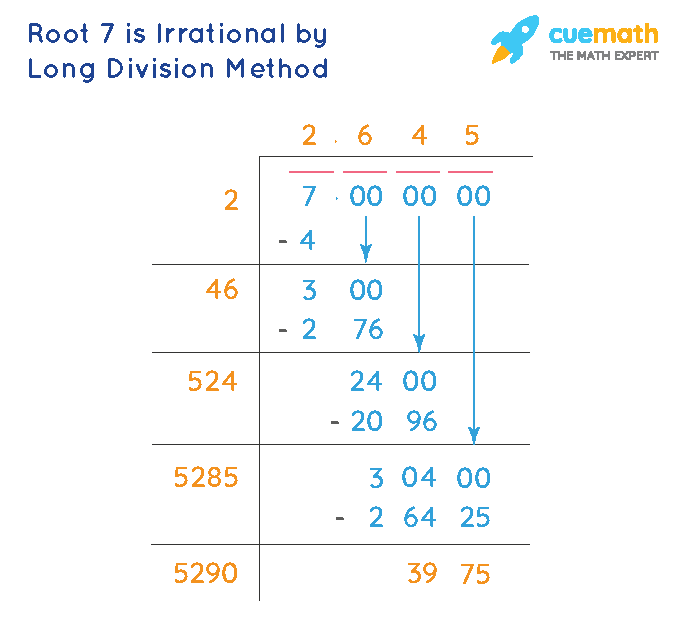
As we can see the value of root 7 does not terminate after 3 decimal places. It can still be extended further. Hence, this makes √7 an irrational number.

☛ Also Check:

•  
• Prove that Root 2 is Irrational
• Prove that Root 3 is Irrational
• Prove that Root 5 is Irrational
• Prove that Root 6 is Irrational
• Prove that Root 11 is Irrational

How do you Prove that Root 7 is Irrational?

We can prove that root 7 is an irrational number by using various methods like the long division method, and method of contradiction. Also, the square root of 7 will be an irrational number if it gives a value after the decimal point that does not terminate and does not repeat. The value of root 7 is 2.64575131106...it is clear that it is non-terminating and nonrepeating, hence √7 an irrational number.

Is 2 times the Square Root of 7 Irrational?

Yes, 2 times the square root of 7 is irrational. To find out whether 2 times the square root of 7 is an irrational number, we multiply both the numbers and check the result. On multiplying 2 with root 7, we get 2 × 2.64575131106... = 5.29150262212.. which is a non-terminating and non-repeating term, therefore the product of the two is an irrational number. 

How to Prove Root 7 is Irrational by Contradiction?

We can prove it by using the contradiction method where we assume the root 7 as the rational number and write it as the ratio of two coprime numbers (p/q) and proceed further if we can find any common factor of the coprime numbers thus assumed, which will prove that the root 7 is irrational.  To prove root 7 is irrational using contradiction we use the following steps:

• Step 1: Assume that √7 is rational.
• Step 2: Hence, √7 = p/q
• Step 3: Now both sides are squared, simplified and a constant value is substituted.
• Step 4: It is found that 7 is a factor of the numerator and the denominator which contradicts the property of a rational number.

Therefore it is proved that root 7 is irrational by the contradiction method. 

Is 3 Times the Square Root of 7 Irrational?

Yes, 3 times the square root of 7 is an irrational number. 3 times the square root 7 is written as 3 × √7 = 3 ×2.64575131106... = 7.93725393318... Here, we get the result that is nonterminating as well as nonrepeating. Thus, we can also conclude that any rational number multiplied with root 7 will be irrational. Hence, 3 times the square root of 7 is irrational too.

How to Prove that 1 by Root 7 is irrational?

We can prove 1 by root 7 is irrational using various methods, such as directly finding the value of 1 by root 7 and checking whether the result is non-terminating and non-recurring or not, or by using the method of contradiction. Let us prove that by finding the value of 1/√7. The value of 1/√7 is 0.377964473.. which extends to infinity and the terms are nonterminating as well as nonrepeating, hence we can clearly say that 1/√7 is an irrational number.