Correlation Coefficient Formula
In statistics, correlation is a way of establishing the relationship/association between two variables. In other words, the correlation coefficient formula helps in calculating the correlation coefficient which measures the dependency of one variable on the other variable. Correlation is measured numerically using the correlation coefficient. The correlation coefficient lies between -1 and 1. A negative correlation coefficient indicates that the relationship between two variables is inverse. A positive correlation coefficient indicates that the value of one variable depends on the other variable directly. A zero-correlation coefficient indicates that there is no correlation between both variables. There are many types of correlation coefficients, among them, the Pearson Correlation Coefficient (PCC) is the most common one. Let us explore how to calculate the correlation coefficient formula for a given population or sample below.
What Is the Correlation Coefficient Formula?
The correlation coefficient is a statistical concept. It establishes a relation between predicted and actual values obtained at the end of a statistical experiment. The correlation coefficient formula helps to calculate the relationship between two variables and thus the result so obtained explains the exactness between the predicted and actual values.
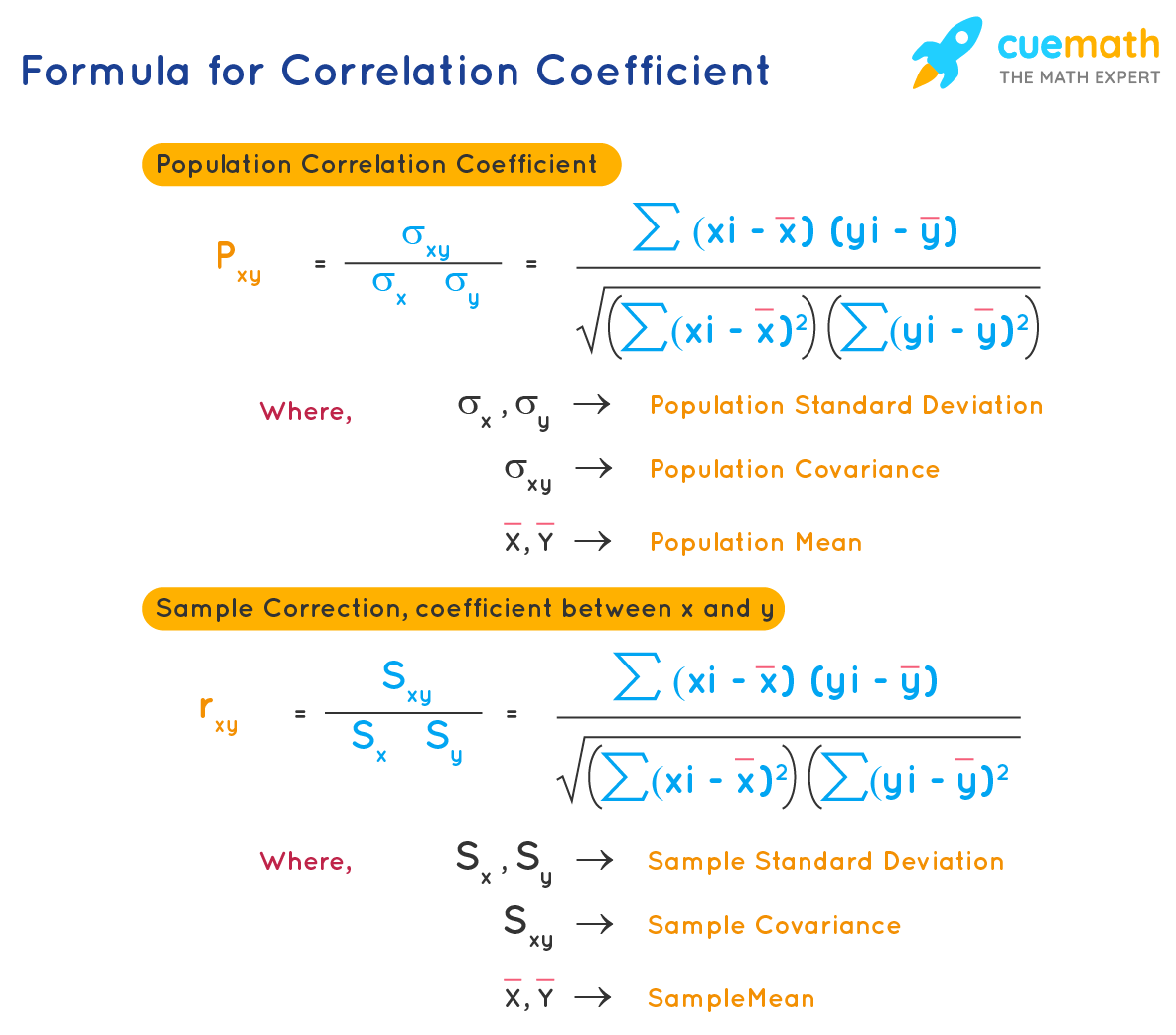
Pearson Correlation Coefficient Formula:
1. Sample Correlation Coefficient
The formula for pearson correlation coefficient for population of size N (written as ρX, Y) is given as:
\(\rho_{X, Y}=\frac{\operatorname{cov}(X, Y)}{\sigma_{X} \sigma_{Y}}=\dfrac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{{\Sigma}_{\Sigma_{i}=1}^{n}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{{\sum}_{\Sigma_{i}=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}}\)
where cov is the covariance and (cov(X,Y)= \(\frac{\sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{N}\), σX is standard deviation of X and σY is standard deviation of Y.
Given X and Y are two random variables.
2. Population Correlation Coefficient
The formula for pearson correlation coefficient for sample of size n (written as rxy) is given as:
\(r_{x, y}=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\Sigma}_{\Sigma_{i}=1}^{n}\left(x_{i}-\bar{x}\right)^{2} \sqrt{\sum}_{\Sigma_{i}=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}\)
where n is the sample size, xi & yi are the ith sample points and x̄ & ȳ are the sample means for the random variables X and Y respectively.
Given X and Y are two random variables.
3. Linear Correlation Coefficient
It uses pearson's correlation coefficient to determine the linear relationship between two variables. Its value lies between -1 and 1. It is given as:
\(r=\frac{n(\Sigma x y)-(\Sigma x)(\Sigma y)}{\sqrt{\left[n \Sigma x^{2}-(\Sigma x)^{2}\right]\left[n \Sigma y^{2}-(\Sigma y)^{2}\right]}}\)
where n is the sample size, xi & yi are the ith sample points and x̄ & ȳ are the sample means for the random variables x and y respectively.
The sign of r indicates the strength of the linear relationship between the variables.
- If r is near 1, then the two variables have a strong linear relationship.
- If r is near 0, then the two variables have no linear relation.
- If r is near -1, then the two variables have a weak (negative) linear relationship.

Let us see the applications of the correlation coefficient formula in the following section.
Examples using Correlation Coefficient Formula
Example 1. Given the following population data. Find the Pearson correlation coefficient between x and y for this data. (Take 1√7 as 0.378)
| x | 600 | 800 | 1000 |
| y | 1200 | 1000 | 2000 |
Solution:
To simplify the calculation, we divide both x and y by 100.
| x/100 | y/100 | \(x_{i}-\bar{x}\) | \(y_{i}-\bar{y}\) | \(\left(\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right)^{2}\) | \(\left(\mathrm{y}_{\mathrm{i}}-\overline{\mathrm{y}}\right)^{2}\) | \((x_i - \bar{x})(y_i - \bar{y})\) |
| 6 | 12 | -2 | -2 | 4 | 4 | 4 |
| 8 | 10 | 0 | -4 | 0 | 16 | 0 |
| 10 | 20 | 2 | 6 | 4 | 36 | 12 |
| \(\bar{x}=8\) | \(\bar{y}=14\) | \(\Sigma\left(x_{i}-\bar{x}\right)^{2}=8\) | \(\Sigma\left(y_{i}-\bar{y}\right)^{2}=56\) | \(\Sigma(x_i-\bar{x})(y_i - \bar{y}) = 16\) |
Using the correlation coefficient formula,
Pearson correlation coefficient for population = \(\frac{\Sigma\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\Sigma\left(x_{i}-\bar{x}\right)^{2} \sum\left(y_{i}-\bar{y}\right)^{2}}}\) = \(\frac{16}{\sqrt{8} \sqrt{56}}\) = \(\frac{2}{\sqrt{7}}\) = 0.756
Answer: Pearson correlation coefficient = 0.756
Example 2. A survey was conducted in your city. Given is the following sample data containing a person's age and their corresponding income. Find out whether the increase in age has an effect on income using the correlation coefficient formula. (Use 1√181 as 0.074 and 1√2091 as 0.07)
| Age | 25 | 30 | 36 | 43 |
| Income | 30000 | 44000 | 52000 | 70000 |
Solution:
To simplify the calculation, we divide y by 1000.
| Age (xi) | Income/1000 (yi/1000) | \(x_{i}-\bar{x}\) | \(y_{i}-\bar{y}\) | \(\left(\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right)^{2}\) | \(\left(\mathrm{y}_{\mathrm{i}}-\overline{\mathrm{y}}\right)^{2}\) | \((x_i - \bar{x})(y_i - \bar{y})\) |
| 25 | 30 | -8.5 | -19 | 72.25 | 361 | 161.5 |
| 30 | 44 | -3.5 | -5 | 12.25 | 25 | 17.5 |
| 36 | 52 | 2.5 | 3 | 6.25 | 9 | 7.5 |
| 43 | 70 | 9.5 | 21 | 90.25 | 441 | 199.5 |
| \(\bar{x}=33.5\) | \(\bar{y}=49\) | \(\Sigma\left(x_{i}-\bar{x}\right)^{2}=181\) | \(\Sigma\left(y_{i}-\bar{y}\right)^{2}=836\) | \(\Sigma(x_i-\bar{x})(y_i - \bar{y}) = 386\) |
Pearson correlation coefficient for sample = \(\frac{\Sigma\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\Sigma\left(x_{i}-\bar{x}\right)^{2} \sum\left(y_{i}-\bar{y}\right)^{2}}}\) = \(\frac{386}{\sqrt{181} \sqrt{836}}\) = \(\frac{193}{\sqrt{181} \sqrt{209}}\) = 0.99
Answer: Yes, with the increase in age a person's income increases as well, since the Pearson correlation coefficient between age and income is very close to 1.
Example 3: Calculate the Correlation coefficient of given data.
| x | 41 | 42 | 43 | 44 | 45 |
| y | 3.2 | 3.3 | 3.4 | 3.5 | 3.6 |
Solution:
Here n = 5
Let us find ∑x , ∑y, ∑xy, ∑x 2, ∑y2
| x | y | xy | x2 | y2 |
|---|---|---|---|---|
| 41 | 3.2 | 131.2 | 1681 | 10.24 |
| 42 | 3.3 | 138.6 | 1764 | 10.89 |
| 43 | 3.4 | 146.2 | 1849 | 11.56 |
| 44 | 3.5 | 154 | 1936 | 12.25 |
| 45 | 3.6 | 162 | 2025 | 12.96 |
| ∑x = 215 | ∑y = 17 | ∑xy = 732 | ∑x2 = 9255 | ∑y2 = 57.9 |
values:
∑x = 215
∑x2 = 9255
x̄ = 43
∑(x - x̄)2 = σσx =10
Y values:
∑y = 17
∑y2 = 57.9
∑(y - ȳ)2 =σσy = 0.1
X and Y combined
N = 5
∑((x - x̄)(y - ȳ)) = 1
∑xy = 732
R calculation:
r = ∑((x - x̄)(y - ȳ))/√((σσx)(σσy))
r = 1/√((10)(0.1)) = 1
Since r = 1, this indicates significant relation between x and y.
FAQs on Correlation Coefficient Formula
What Is Correlation Coefficient Formula in Statistics?
The correlation coefficient formula determines the relationship between two variables in a dataset and thus checks for the exactness between the predicted and actual values.
How To Use Correlation Coefficient Formula?
We can use the coefficient correlation formula to calculate the Pearson product-moment correlation,
- Step 1: Determine the covariance of the two given variables.
- Step 2: Calculate the standard deviation of each variable.
- Step 3: Divide the covariance by the product of the standard deviations of two variables.
What Is n in the Correlation Coefficient Formula?
In the coefficient correlation formula, n refers to the sample size.
- Sample Correlation Coefficient: \(\rho_{X, Y}=\frac{\operatorname{cov}(X, Y)}{\sigma_{X} \sigma_{Y}}=\frac{\Sigma_{i=1}^{N}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\Sigma_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}}^{N} \sum_{\Sigma_{i}=1}^{N}\left(Y_{i}-\bar{Y}\right)^{2}}\)
- Population Correlation Coefficient: \(r_{x, y}=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\Sigma}_{\Sigma_{i}=1}^{n}\left(x_{i}-\bar{x}\right)^{2} \sqrt{\sum}_{\Sigma_{i}=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}\)
- Linear Correlation Coefficient: \(r=\frac{n(\Sigma x y)-(\Sigma x)(\Sigma y)}{\sqrt{\left[n \Sigma x^{2}-(\Sigma x)^{2}\right]\left[n \Sigma y^{2}-(\Sigma y)^{2}\right]}}\)
What Are the Applications of Correlation Coefficient Formula?
Given below are the most important applications of the coefficient correlation formula:
- The coefficient correlation formula helps in the analysis of the given data by quantifying the degree to which two variables are related which further depicts a linear relationship between two variables.
- It is used for financial analysis as it determines the relationship between data sets in business and thus, in a way support decision making.
- It helps a lot in decision-making in various fields as it helps to understand the strength of the relationship between two different variables.
visual curriculum