A day full of math games & activities. Find one near you.

Angle between a Line and a Plane

In classical mathematics, analytic geometry, the angle between the line and the plane is equal to the complement of the angle between the line and the normal. Under this topic on 2D geometry, let us first define a straight line and a plane and how the angle between a line and a plane is determined.

1.	What is a Straight Line?
2.	What is a Plane?
3	The Angle Between a Line and a Plane
4.	Solved Examples
5.	Practice Questions
6.	FAQs

What is a Straight Line?

Where do we find straight lines in real life? A pencil, pen, straight road; the edge of the ruler, building, hands of clocks, etc. are few examples of it. A straight line is a simple 2D geometrical shape with a set of points that has no breadth. It extends in both directions with no endpoints and only has length. And, so the length of a line is infinite and it has no height or width, making it a part of 2-D geometry.

Lines can be parallel, perpendicular, intersecting, or concurrent.

Lines

What is a Plane?

A plane is also a 2D geometric surface that does not have any thickness but only length and width. A plane is formed when an infinite number of points extend infinitely in either direction to form a flat surface.
In geometry, a plane is obtained when a set of lines are arranged adjacent to each other. If we draw something on flat paper, then it means that we are drawing something on a plane.

The Angle between a Line and a Plane

While a plane is a two-dimensional surface measured in terms of length and width, the straight line has one dimension which is measured in terms of length. A line forms an angle with the plane at the point of contact when that line is an incident on a plane which is said to be the angle between a line and a plane. Simply, it can be defined as the angle between the line and its projection onto this plane.

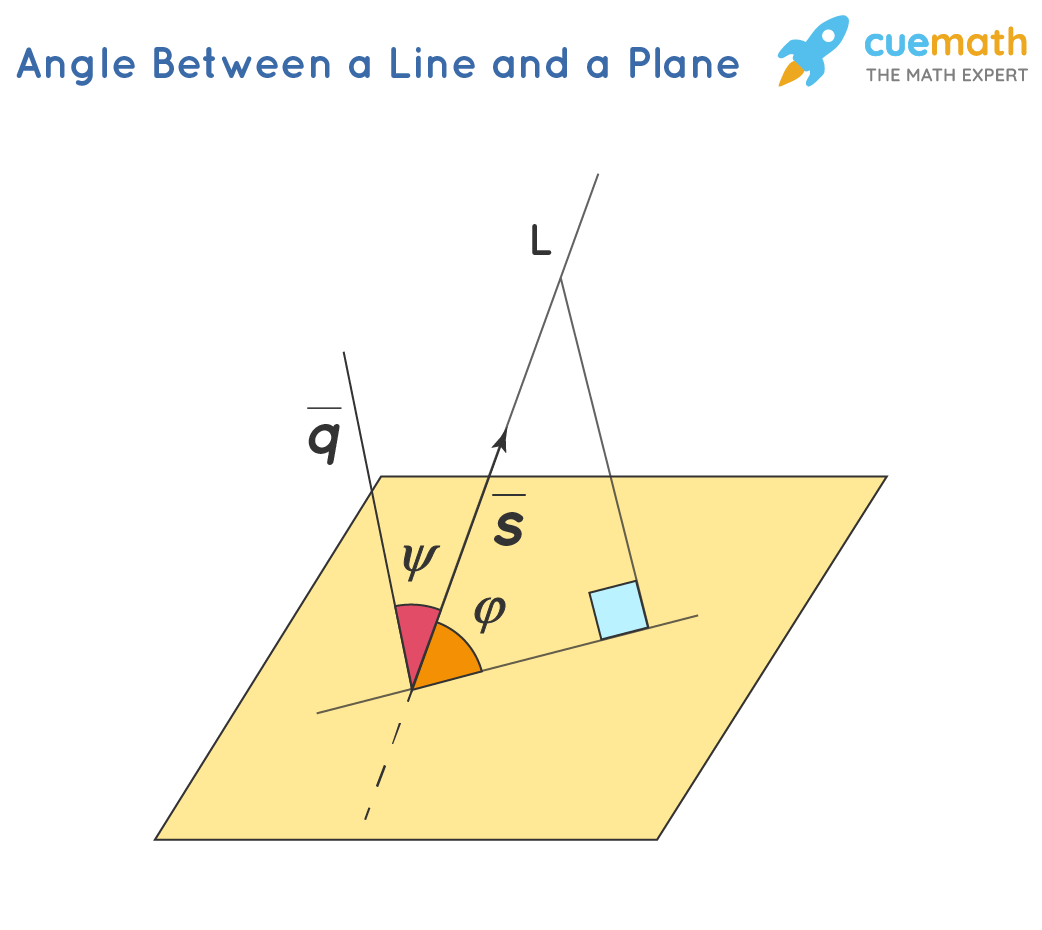
Angle Between a Line and a Plane

Consider this direction vector of line L in space, \(\bar{s}\)=〈 l ; m ; n〉 , where l, m and n represent the x, y and z components of the s vector,.and equation of the plane \(\mathrm{A} x+\mathrm{B} y+\mathrm{C} z+\mathrm{D}=0\) then the angle between this line and plane can be found using this formula \(\sin \varphi=\frac{|\mathrm{A} \cdot l+\mathrm{B} \cdot m+\mathrm{C} \cdot n|}{\sqrt{\mathrm{A}^{2}+\mathrm{B}^{2}+\mathrm{C}^{2}} \cdot \sqrt{{l^{2}+m^{2}+n^{2}}}}\)

Important Notes

The angle between a plane and a line can be defined as the angle between the line and its projection onto the plane.
Straight lines can be parallel, perpendicular, or intersecting

Example 1:

If the angle \(\theta\) between the line \(\frac{x+1}{1}=\frac{y-1}{2}=\frac{z-2}{2}\) and the plane \(2 x-y+\sqrt{\lambda} z+4=0\) is such
that \(\sin \theta=\frac{1}{3}\), then find the value of \(\lambda\).

Solution :

Given: Symmetric equations of the line = \(\frac{x+1}{1}=\frac{y-1}{2}=\frac{z-2}{2}\)
Compairing it with the equation \(\frac{x+x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}\)

Hence, for the line, 〈 l ; m ; n〉 = 〈 1 ; 2 ; 2〉

Angle between line and plane is:
\(\begin{aligned}&\sin \left(\theta\right)=\frac{2-2+2 \sqrt{\lambda}}{3 \times \sqrt{5+\lambda}}, \text { where } \theta \text { is angle between line and plane }\\
&\Rightarrow \sin \theta=\frac{2 \sqrt{\lambda}}{3 \sqrt{5+\lambda}}=\frac{1}{3}\\
&\Rightarrow 4 \lambda=5+\lambda\\
&\Rightarrow \lambda=\frac{5}{3}
\end{aligned}\)
Example 2: Find the angle between the planes \(\overrightarrow{\mathrm{r}} .(\hat{\mathrm{i}}-2 \hat{\mathbf{j}}+3 \hat{\mathrm{k}})=5\) and the line\(\overrightarrow{\mathrm{r}}=(\hat{\mathrm{i}}+\hat{\mathbf{j}}-\hat{\mathrm{k}})+
\lambda(\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}})\)

Solution :

Given, equation of plane: \(\overrightarrow{\mathrm{r}} .(\hat{\mathrm{i}}-2 \hat{\mathbf{j}}+3 \hat{\mathrm{k}})=5\)

Compairing it with, \(\overrightarrow{\mathrm{r}} .\hat{n}=d\), where \(\hat{n} \) is the normal vector to the plane.

Hence finding the angle between the normal vector of the plane and the line.
\(\begin{aligned} &\cos \theta=\frac{1 \times 1+-2 \times-1+3 \times 1}{\sqrt{\left(1^{2}+2^{2}+3^{2}\right)\left(1^{2}+1^{2}+1^{2}\right)}}=\frac{\sqrt{42}}{7} \Rightarrow 0=\cos ^{-1} \frac{\sqrt{42}}{7}\end{aligned}\)
Since the angle between line and plane is the complement of the angle between the line and plane's normal vector.
Therefore, angle between plane and line = \(\begin{aligned}90-\theta=90-\cos ^{-1}\left(\frac{\sqrt{42}}{7}\right)=67.79^{\circ}\end{aligned}\)

go to slide go to slide

Have questions on basic mathematical concepts?

Become a problem-solving champ using logic, not rules. Learn the why behind math with ourCuemath’s certified experts.

Book a Free Trial Class

go to slide go to slide go to slide

FAQs on Angle Between a Line and a Plane

Can a Point be a Line?

A point is indicated by a dot. A line can be defined as a collection of points that extends infinitely from both ends. It has one dimension, which is the length. The points that fall on the same line are called Collinear points.

What Does a Line Mean?

A line can be defined as a straight 1D figure that has no thickness and extends endlessly in both directions. And, it is most often described as the shortest distance between any two points.

What are the Two Classifications of Straight Lines?

Straight lines are classified into horizontal and vertical lines. The types of lines also include are parallel lines, intersecting lines, and perpendicular lines.

Can an Angle be a Straight Line?

A straight angle is an angle equal to 180 degrees and a straight angle is also called a flat angle. Since it actually appears as a straight line, it is called a straight angle.

How many Dimensions does a Plane have?

Planes are two-dimensional, but they can exist in three-dimensional space too.

Download FREE Study Materials

Angles Worksheet

Math worksheets and
visual curriculum