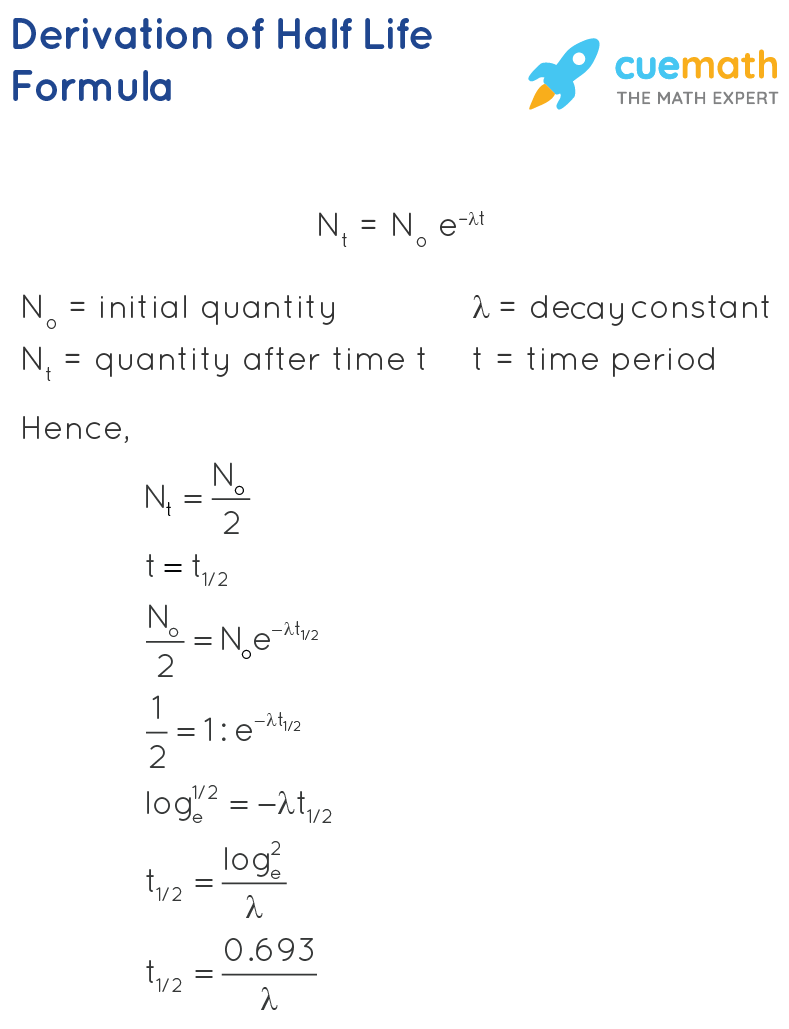Half Life Formula

The half-life formula is used to find the half-life of a substance that is decaying or reducing in quantity. A substance that is decaying has a different rate of decay for different quantities of the substance. As the quantity of the substance reduces the rate of decay also slows down, and hence it is very difficult to find the life of a decaying substance. Therefore the half-life formula is used to provide the right metrics to define the life of decaying material. In this section, let us learn more about the half life formula and solve a few examples.

What is Half Life Formula?

Half-life refers to the amount of time it takes for half of a particular sample to react i.e it refers to the time that a particular quantity requires to reduce its initial value to half. The half-life formula is commonly used in nuclear physics where it describes the speed at which an atom undergoes radioactive decay. The formula for the half-life is obtained by dividing 0.693 by the constant λ. Here λ is called the disintegration or decay constant. Hence the formula to calculate the half-life of a substance is:

\(t_{\frac{1}{2}} = \dfrac{0.693}{\lambda} \)

Where, 

\(t_{\frac{1}{2}}\) = half-life

λ = constant

Half Life Formula

Let N be the size of the population of the radioactive atoms at a given time t, dN be the amount by which it decreases in time dt. The rate of change is given as dN/dt = -λN, where λ is the decay constant.

On integrating this equation, we get N = \(N_0\)e^-λt , where \(N_0\) = the size of the initial population of radioactive atoms at t = 0. This shows that the population decays exponentially at a rate that depends on λ. The time taken for half of the original population of radioactive atoms to decay is called the half-life. This relationship between half-life, the time period, t^1/2, and the decay constant λ is given by \(t_{\frac{1}{2}} = \dfrac{0.693}{\lambda} \).

Examples Using Half Life Formula

Example 1: The decay constant of a substance is 0.84 s^-1. Find the half life of the substance.

Solution:

Given decay constant λ = 0.84 
The half life formula can be used to find the half life of the substance.
\(t_{\frac{1}{2}}\) = 0.693/λ

= 0.693/0.84

= 0.825

Therefore, the half life of the substance is 0.8 seconds.

Example 2: Find the value of the decay constant of a radioactive substance having a half-life of 0.04 seconds.

Solution:

Given half life of the substance is \(t_{\frac{1}{2}}\)= 0.04
The half life formula can be used to find the half life of the substance.
\(t_{\frac{1}{2}}\) = 0.693/λ

λ= 0.693/0.04

= 17.325
Therefore, the decay constant of the radioactive substance is 17.325 s^-1.

Example 3: Calculate the half-life of a radioactive substance whose disintegration constant happens to be 0.004 1/years?

Solution: 

The quantities available here are,

λ= 0.004  1/years

Using the half life formula, 

\(t_{\frac{1}{2}}\) = 0.693/λ

=0.693/0.004

= 173.25

Hence, the half-life of this particular radioactive substance is 173.25 years.