Lateral Area of a Square Pyramid
The lateral area of a square pyramid is defined as the area covered by its slant of lateral faces. A pyramid is a three-dimensional object whose base can be any polygon whereas its side faces are all congruent triangles. One side of each of these triangles coincides with one side of the base polygon. The pyramids are named according to the shape of their bases. A square pyramid is a pyramid whose base is a square. Just like other three-dimensional shapes, a square pyramid also has two types of areas.
- Lateral Surface Area (LSA)
- Total Surface Area (TSA)
Let us learn about the lateral area of a square pyramid along with the formula and a few solved examples here. You can find a few practice questions also to practice at the end.
| 1. | What Is the Lateral Area of a Square Pyramid? |
| 2. | Formula of Lateral Area of a Square Pyramid |
| 3. | How to Calculate Latera Area of Square Pyramid? |
| 4. | FAQs on Lateral Area of a Square Pyramid |
What Is the Lateral Area of a Square Pyramid?
The word "lateral" means "belonging to the side". So the lateral area of a square pyramid is the sum of the areas of its side faces. This is also known as the lateral surface area (LSA) of the square pyramid. We know that a square pyramid has:
- a base which is a square.
- 4 side faces, each of which is a triangle.
All these triangles are congruent and isosceles each of which has a side that coincides with a side of the base (square).
So, the lateral surface area of a square pyramid is the sum of the areas of four of its triangular side faces.
Formula of Lateral Area of a Square Pyramid
Let us consider a square pyramid whose base's length (square's side length) is 'a' and the height of each side face (triangle) is 'l' (this is also known as the slant height). i.e., the base and height of each of the 4 triangular faces are 'a' and 'l' respectively. So the area of each such triangular face is 1/2 × a × l. So the sum of areas of all 4 triangular faces is, 4 ( ½ al) = 2 al. Thus, the lateral area of a square pyramid = 2al
What if we are given the height of the pyramid instead of giving the slant height? Let us assume that the height of the pyramid (altitude) be 'h'. Then by applying Pythagoras theorem (you can refer to the below figure),
l=√[(a2/4) + h2]
Substituting this in the above formula,
The lateral area of a square pyramid = 2al = 2a√[(a2/4) + h2]
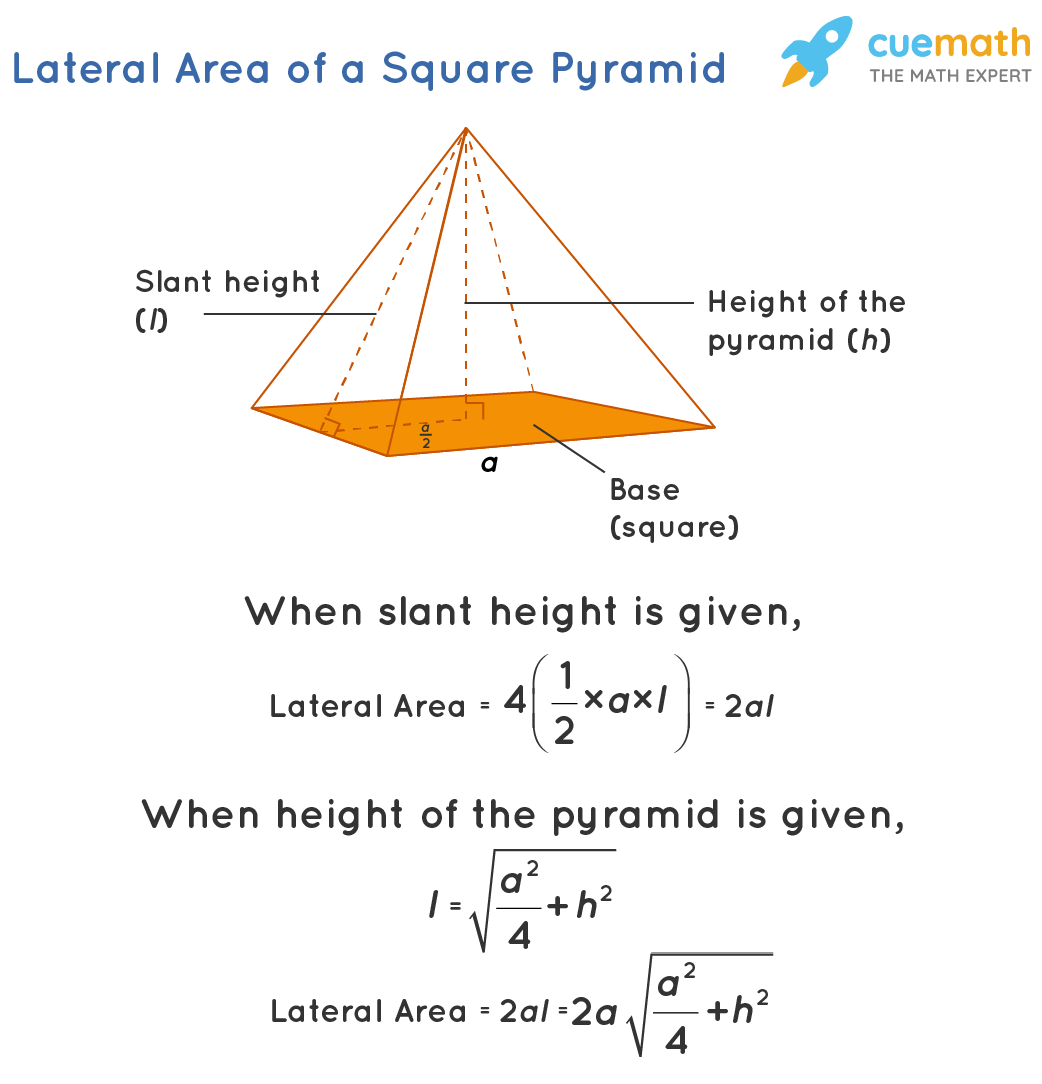
Note: √[(a2/4) + h2] can be simplified as (1/2)√(a2 + 4h2). Thus, the formula of lateral area of a square pyramid can be written as 2a[(1/2)√(a2 + 4h2)] = a√(a2 + 4h2).
How to Calculate the Lateral Area of a Square Pyramid?
The surface area of a lateral pyramid can be calculated following the given steps,
- Note the given dimensions of the square pyramid and check they should have the same units.
- Apply the formula to calculate the lateral area of square pyramid,
Lateral area of a square pyramid = 2al = 2a√[(a2/4) + h2], where, 'a' is base length, 'h' is height and 'l' is slant height of the sqaure pyramid. - Express the answer with square units.
Now that we have understood the lateral area of a square pyramid, let us have a look at a few solved examples to understand better.
Solved Examples on Lateral Area of a Square Pyramid
-
Example 1: Find the lateral area of a square pyramid of base length 10 cm and slant height 16 cm.
Solution:
The base length of the square pyramid is, a = 10 cm.
Its slant height is, l = 16 cm.
The lateral area = 2al = 2 (10) (16) = 320 cm2
Answer: The lateral area of the given square pyramid = 320 cm2.
-
Example 2: The base area of a square pyramid is 256 square units and its height (altitude) is 25 units. Find its lateral area. Round off your answer to the nearest hundredth.
Solution:
Let the side of the base (square) be 'a' units.
Then it is given that a2 = 256 ⇒ a = 16 units.
The height of the given square pyramid is, h = 25 units.
Using lateral area of a square pyramid formula,
Lateral area = 2a√[(a2/4) + h2]
= 2 (16) √(162/4) + 252] ≈ 839.96 square units.
The final answer is rounded to the nearest hundredth.
Answer: The lateral area of the given square pyramid = 839.96 square units.

FAQs on Lateral Area of a Square Pyramid
What Is the Lateral Area of the Square Pyramid?
The lateral area of a square pyramid is the sum of the areas of all its 4 triangular side faces. If a, h, and l are the base length, the height of the pyramid, and slant height respectively, then the lateral area of the square pyramid = 2al (or) 2a√[(a2/4) + h2].
How Do You Find the Lateral Surface Area of a Square Pyramid?
To find the lateral area of a square pyramid, find the area of one side face (triangle) and multiply it by 4. If a and l are the base length and the slant height of a square pyramid, then lateral area of the square pyramid = 4 (½ × a × l) = 2al. If h is the height of the pyramid, then the lateral area = 2a√[(a2/4) + h2].
What Is the Area of One of the Triangular Faces of a Square Pyramid?
If a and l are the base length and the slant height of a square pyramid, then the area of one of the 4 triangular side faces is, ½ × a × l.
How Do You Find the Lateral Surface Area and Total Surface Area of a Square Pyramid?
The lateral surface area of a square pyramid is the sum of the areas of the side faces only, whereas the surface area is the lateral area + area of the base. The lateral area of a square pyramid = 2al (or) 2a√[(a2/4) + h2].
To get the surface area, we need to add the area of the base (which is a2) to each of these formulas. The surface area of a square pyramid = a2 + 2al (or) a2 + 2a√[(a2/4) + h2].
where,
- a = Length of the base (square)
- l = slant height
- h = height of the pyramid
How to Find the Lateral Area of a Square Pyramid With Slant Height?
Lateral area of square pyramid using the slant height can be calculated as, Lateral area of a square pyramid = 2al, where, 'a' is base length and 'l' is slant height of the sqaure pyramid.
visual curriculum