Surface Area of Trapezoidal Prism

The surface area of a trapezoidal prism is the amount of area occupied by the surface of a trapezoidal prism. A trapezoidal prism is a three-dimensional solid that is made up of two trapezoids on opposite faces which are joined by four rectangles called the lateral faces. Like all three-dimensional shapes, you will learn how to calculate the surface area of a trapezoidal prism. Let's explore and learn more about the surface area formula of a trapezoidal prism using solved examples.

The area occupied by the surface of a trapezoidal prism is known as the surface area of a trapezoidal prism. Since the trapezoidal prism has a flat base, thus we can say that it has a total surface area and a curved surface area. The surface area of any three-dimensional geometrical shape is the sum of the surfaces of that enclosed solid which equals the areas of all of the faces. A trapezoidal prism has two trapezoidal faces four rectangular faces. Thus, the simple formula for calculating the surface area of a trapezoidal prism involves the area of the base, the perimeter of the base, and the slant height of any side of the prism. The surface area of any geometric figure is always measured in square units like cm², m², ft, or cubits².

As a trapezoidal prism also has a curved surface, thus we can express its total surface area as well as the curved surface area. A trapezoidal prism has two kinds of surface area:

• Total Surface Area
• Curved/Lateral Surface Area

The surface area of a trapezoidal prism can be given with this formula: (b1+b2)h + PH. In this formula, "b1" and "b2" stand for the length of the bases of the trapezoid. The height of the trapezoid is "h". The perimeter of the trapezoid is "P", and "H" is the height of the prism.

• Total Surface Area = The total surface area of a prism is the sum of the areas of its lateral faces and its two bases = (b1+b2)h + PH or 2B + PH
• Lateral Surface Area = The lateral surface area of a prism is the sum of the areas of its lateral faces = (a+b+c+d) × H or PH

We know that the base of a prism is in the shape of a trapezoid. Here,

• b and d are parallel sides.
• h is the distance between the parallel sides.
• l is the length of the trapezoidal prism.

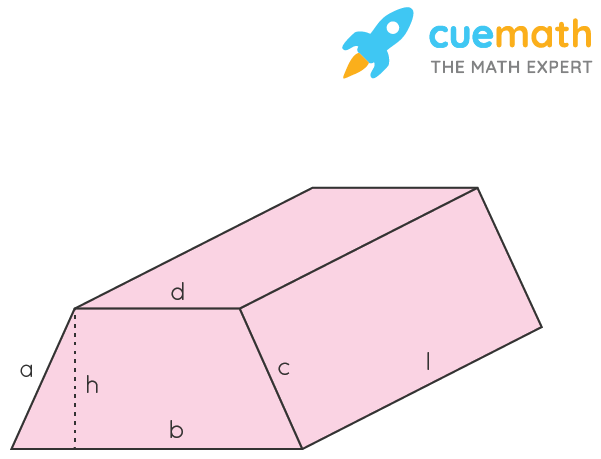
We already know that the total surface area of the trapezoidal prism (TSA) = 2 × area of base + lateral surface area ---- (1)
Also, the area of a trapezoid = height(base1 × base 2)/2. Thus, the area of trapezoidal base = h (b + d)/2 ---- (2)

The lateral surface area of the trapezoidal prism (LSA) is the sum of the areas of each rectangular surface around the base that means, LSA = (a × l) + (b × l) + (c × l) + (d × l) ---- (3)

Substituting the values from equation (2) and equation (3) in the TSA formula, which is represented by equation (1):
Therefore, the total surface area of the trapezoidal prism (TSA) = 2 × h (b + d)/2 + (a × l)+(b × l) + (c × l) + (d × l) = h (b + d) + [(a × l) + (b × l) + (c × l) + (d × l)]

TSA of the trapezoidal prism = h (b + d) + l (a + b + c + d).

Thus, the total surface area of a trapezoidal prism is h(b+d)+l(a+b+c+d) square units.

Here are the steps to calculate the surface area of a trapezoidal prism. Note that all measurements are of the same units.

• Step 1: Identify the four sides of the trapezium - a, b, c, and d, representing the widths of the four rectangles. Add these 4 values in order to find the perimeter P.
• Step 2: Identify the length H of the prism.
• Step 3: Put the values in the formula, (a+b+c+d) × H or PH, to find the lateral surface area of the hexagonal prism.
• Step 4: Identify b1 and b2 (lengths of the bases) of the trapezoid and h (height) of the trapezoid. Find the base area B by putting the above values in the formula, (b1+b2)h/2
• Step 5: Put the values in the formula, 2B + Lateral Surface Area(PH), to get the total surface area of the hexagonal prism.

Now refer to the example given below.

Example: Determine the total surface area of the trapezoidal prism.

Solution: Using the Pythagoras theorem, the slant height or the non-parallel side = √(16+1) = √17 = 4.123 ft

The perimeter of the base is the sum of the lengths of the sides. Thus, P = (4.123 + 4 + 6 + 4.123) = 18.246 ft

Area of base = 1/2(b1+b2)h = 1/2(3+6)4 = 18 sq ft
T.S.A.= Ph+2B =  18.246 × 9 + 2 ×18 =200.214 sq feet.

Related Topics

Listed below are a few interesting topics related to the surface area of trapezoidal prism, take a look:

• Surface Area of Prism
• Volume of Trapezoidal Prism
• Surface Area of a Prism Calculator

What is the Surface Area of a Trapezoidal Prism?

The surface area of a trapezoidal prism refers to the amount of area occupied by the surface of a trapezoidal prism. As a trapezoidal prism has a curved surface as well, thus we can express its curved surface area as well as total surface area. The unit of the surface area of a trapezoidal prism is given in cm², m², ft, or cubits².

What is the Formula to Calculate the Surface Area of Trapezoidal Prism?

As the total surface area of a trapezoidal prism is the sum of the areas of its lateral faces and its two bases, thus, the formula to calculate the total surface area of the trapezoidal prism is (b1+b2)h + PH. Since it has a lateral surface as well which is calculated as the sum of the areas of its lateral faces. Thus, the lateral surface area of the trapezoidal prism is (a+b+c+d) × H

How to Calculate the Total Surface Area of a Trapezoidal Prism?

To calculate the total surface area of the prism, follow the steps given below:

• Step 1: Check for the four sides of the trapezium - a, b, c, and d and add them to find the perimeter P.
• Step 2: Identify the length H of the prism.
• Step 3: Add the respective values in the formula, (a+b+c+d) × H or PH, and you will get the lateral surface area of the hexagonal prism.
• Step 4: Identify b1 and b2 (lengths of the bases) of the trapezoid and h (height) of the trapezoid. Then put the above values in the formula, (b1+b2)h/2 to find the trapezoid base area.
• Step 5: Put the values in the formula, (b1+b2)h + Lateral Surface Area(PH), to obtain the final value of the total surface area of the hexagonal prism.
• Step 6: Add units as well with the final value so obtained.

How to Find the Lateral Surface Area of Trapezoidal Prism?

We can find the lateral surface area of the prism using the below-given steps:

• Step 1: Find the base perimeter of the given trapezoidal prism.
• Step 2: Identify the length of the prism.
• Step 3: Multiply the perimeter and the length. (a+b+c+d) × H
• Step 4: Write the product value with square units.

What Happens to the Total Surface Area of Trapezoidal Prism If Its Height is Doubled?

We already know that the total surface area of a trapezoidal prism is (b1+b2)h + PH. Thus, if its height will be doubled, it will lead to an increase in its surface area but this will not lead to its surface area getting doubled.

How to Calculate the Surface Area of Right Trapezoidal Prism?

The following steps will help us calculate the surface area of a right trapezoidal prism:

• Step 1: As depicted from the trapezoidal prism shape, the width of the four rectangles is the same as the length, H of the prism.
• Step 2: The length of the four rectangles equals the sum of the four sides of the trapezoid, the two bases, and the other two sides, which gives the perimeter P of the trapezoid.
• Step 3: The product of the sum of two bases (b1 and b2) and the height h of the prism divided by 2, gives the base area B.
• Step 4: The surface area can be given with the formula: (b1+b2)h + PH.

How to Find the Surface Area of an Isosceles Trapezoidal Prism?

To find the surface area of an isosceles trapezoidal prism,

• Step 1: Find perimeter: The perimeter of the base of the trapezoidal prism is the sum of the lengths of the sides.
• Step 2: The base is an isosceles trapezoid, thus its area B is 1/2h(b1+b2).
• Step 3: Put the values in the formula, T.S.A.= PH+2B