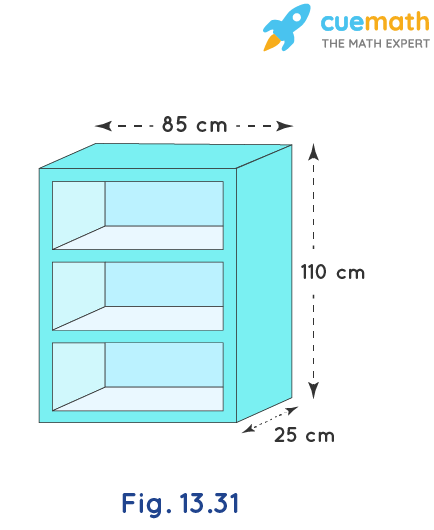
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see Fig. 13.31). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
Solution:
Since the bookshelf is cuboidal in shape and opened at the front with three shelves of the same dimensions, the area to be polished will be 5 surfaces of cuboidal bookshelf and the front border with plank’s thickness.
The area to be painted will be 3 shelves of the bookshelf with internal dimensions and the area of each shelf will be 5 surfaces of the cuboidal shelf.
We can calculate the total cost of polishing and painting by multiplying the rate and their respective area.
The Volume of a cuboid of length l, breadth b, and height h, is = l × b × h
External measures of the bookshelf is,
Breadth, B = 85 cm
Depth, D = 25 cm
Height, H = 110 cm
The thickness of the plank, t = 5 cm
Internal measures of the bookshelf is,
The breadth of each shelf, b = B - 2t
⇒ b = 85 cm - 2 × 5 cm = 75 cm
Depth of each shelf, d = D - t
⇒ d = 25 cm - 5 cm = 20 cm
Height of each shelf, h = H - 4t
= (110 cm - 4 × 5 cm) ÷ 3
= 90 cm / 3 = 30 cm
Now, Surface area to be polished = External 5 surfaces of the bookshelf + border of the shelf
= 2(B + H) D + BH + 2Ht + 4bt
= [2 × (85 cm + 110 cm) × 25 cm] + (85 cm × 110 cm) + (2 × 110 cm × 5 cm) + (4 × 75 cm × 5 cm)
= 9750 cm2 + 9350 cm2 + 1100 cm2 + 1500 cm2
= 21700 cm2
Cost of polishing at the rate of 20 paise per cm2 = 21700 cm2 × (₹ 20/100) / cm2 = ₹ 4340
Surface area to be painted = Internal 5 surfaces of 3 shelves
= 3 [2(b + h)d + bh]
= 3 [2 × (75 cm + 30 cm) × 20 cm + (75 cm × 30 cm)]
= 3 [4200cm2 + 2250 cm2]
= 3 × 6450 cm2
= 19350 cm2
Cost of painting at the rate of 10 paise per cm2 = 19350 cm2 × (₹ 10/100) / cm2 = ₹ 1935
Total expense required for polishing and painting = ₹ 4340 + ₹ 1935 = ₹ 6275
Thus, the total expense required for polishing and painting the surface of the bookshelf is ₹ 6275.
☛ Check: NCERT Solutions for Class 9 Maths Chapter 13
Video Solution:
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see Fig. 13.31). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm² and the rate of painting is 10 paise per cm², find the total expenses required for polishing and painting the surface of the bookshelf.
NCERT Solutions for Class 9 Maths Chapter 13 Exercise 13.9 Question 1
Summary:
It is given that the wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm with the thickness of the plank as 5 cm everywhere. If the external faces are to be polished and the inner faces are to be painted given the rate of polishing is 20 paise per cm² and the rate of painting is 10 paise per cm², we have found that the total expense required for polishing and painting the surface of the bookshelf is ₹ 6275.
☛ Related Questions:
- The front compound wall of a house is decorated by wooden spheres of diameter 21cm, placed on small supports as shown in Fig 13.32. Eight such spheres are used for this purpose and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm².
- The diameter of a sphere is decreased by 25%. By what percent does its curved surface area decrease?
- Twenty-seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S′. Find the i) Radius r′ of the new sphere, ii) Ratio of S and S′.
- A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much Medicine (in mm3) is needed to fill this capsule?
visual curriculum