Find the values of the unknowns x and y in the following diagrams:
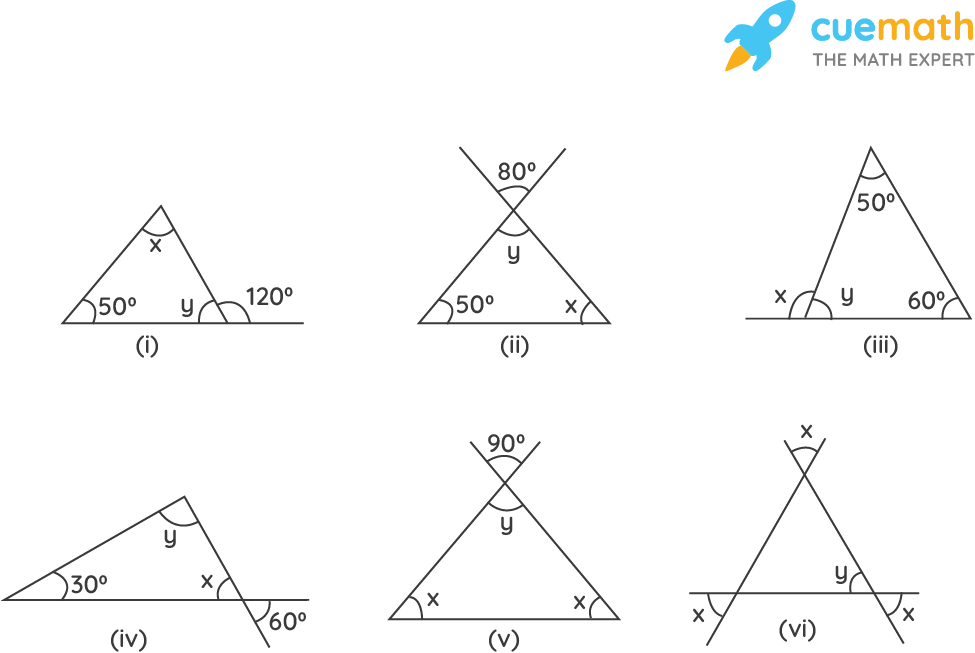
Solution:
(i) Let us assume the unknown interior angle of the given triangle as x and y.
Now, let us model this problem visually.
1. We know that according to the exterior angle theorem, the exterior angle of a triangle is the sum of interior opposite angles.
2. As we know that the sum of the interior angles of a triangle is always equal to 180 degrees.
We know that, the sum of interior opposite angles of a triangle = Exterior angle
50° + x = 120°
x = 120° − 50°
x = 70°
Sum of interior angles = 50° + 70° + y = 180°
120° + y = 180°
y = 180° − 120°
y = 60°
(ii) This question is based on two concepts.
First vertically opposite angles are equal. By using this, we can find out the angle opposite to 80° that is one of the interior angles.
Now, one more interior angle is unknown here. So, we use the angle sum property, that is, the sum of three interior angles of a triangle is 180°, and find out the value of another unknown angle.
y = 80°(vertically opposite angles)
By angle sum property,
Sum of interior angles = 50° + x + y = 180°
50° + x + 80° = 180°
130° + x = 180°
x = 180° − 130°
x = 50°
(iii) Visually identify the unknown interior angle and then follow two steps.
First, by using the angle sum property, we can find out the value of the unknown interior angle, and then for angle x, we know that sum of interior opposite angles of a triangle is equal to the exterior angle.
We know that, sum of interior opposite angles of a triangle = Exterior angle
50° + 60° = 𝑥
110° = 𝑥
𝑥 = 110°
By angle sum property,
Sum of interior angles = 50° + 60° + 𝑦 = 180°
110° + 𝑦 = 180°
𝑦 = 180° − 110°
𝑦 = 70°
(iv) This question is based on two concepts.
Vertically opposite angles are equal. By using this, we can find out the angle opposite to 60°, that is, one of the interior angles.
Now, one more interior angle is unknown here so, we use the angle sum property i.e. sum of three interior angles of a triangle is 180°, and find out the value of another unknown angle.
x = 60°(vertically opposite angles are equal)
We know that, Sum of interior angles of a triangle =180°
30° + 𝑥 + 𝑦 = 180°
30° + 60° + y = 180°
90° + y = 180°
y = 180° − 90°
y = 90°
(v) This question is based on two concepts.
Vertically opposite angles are equal. By using this we can find out the value of one interior angle, and then by applying the angle sum property we can find out another interior angle.
Here the measure of two interior angles is equal.
y = 90°(vertically opposite angles are equal)
We know that,
Sum of interior angles of a triangle = 180°
y + x + x = 180°
90° + 2x = 180°
2x = 180° − 90°
x = 90/2
x = 45°
(vi) Vertically opposite angles are equal. By using this, we can find out that x and y are equal and then by applying the angle sum property we can find all angles.
x = y (vertically opposite angles are equal)
We know that, Sum of interior angles of a triangle =180°
x + x + y = 180°
2x + y = 180°
2x + x = 180° (x = y since they are vertically opposite angles)
3x = 180°
x = 180/3
x = 60
Since x = y, y = 60°
☛ Check: NCERT Solutions for Class 7 Maths Chapter 6
Video Solution:
Find the values of the unknowns x and y in the following diagrams:
NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.3 Question 2
Summary:
The values of the unknowns x and y in the following diagrams are: (i)x = 70°, y = 60°; (ii) x = 50°,y = 80° ; (iii) x = 110° , y = 70° ; (iv) x = 60° , y = 90° ; (v) x = 45° , y = 90° ; (vi) x = 60°, y = 60°
☛ Related Questions:
visual curriculum