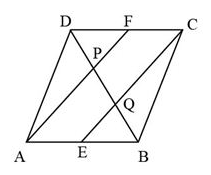
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig.8.31). Show that the line segments AF and EC trisect the diagonal BD.

Solution:

Given: In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively.

To Prove: Line segments AF and EC trisect the diagonal BD.

According to the converse of mid-point theorem, we know that a line drawn through the mid-point of any side of a triangle that is parallel to another side bisects the third side.

ABCD is a parallelogram.

AB || CD

Hence, AE || FC

Again, AB = CD (Opposite sides of parallelogram ABCD)

⇒ 1/2 AB = 1/2 CD

⇒ AE = FC (E and F are mid-points of side AB and CD)

In quadrilateral AECF, one pair of opposite sides (AE and CF) is parallel and equal to each other.

Therefore, AECF is a parallelogram.

∴ AF || EC (Opposite sides of a parallelogram)

In ΔDQC, F is the mid-point of side DC and FP ||CQ (as AF || EC).

Therefore, by using the converse of the mid-point theorem, it can be said that P is the mid-point of DQ.

∴ DP = PQ --------------- (1)

Similarly, in ΔAPB, we know E is the mid-point of side AB and thus, EQ || AP (as AF || EC).

Therefore, by using the converse of the mid-point theorem, it can be said that Q is the mid-point of PB.

∴ PQ = QB --------------- (2)

From equations (1) and (2),

DP = PQ = BQ

Hence, the line segments AF and EC trisect the diagonal BD.

☛ Check: NCERT Solutions Class 9 Maths Chapter 8

---

Video Solution:

In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig.8.31). Show that the line segments AF and EC trisect the diagonal BD
 

NCERT Maths Solutions Class 9 Chapter 8 Exercise 8.2 Question 5

Summary:

If in a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively, then the line segments AF and EC trisect the diagonal BD.

---

☛ Related Questions:

• ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig. 8.29). AC is a diagonal. Show that:(i) SR || AC and SR = 1/2AC(ii) PQ = SR(iii) PQRS is a parallelogram.
• ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
• ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
• ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC