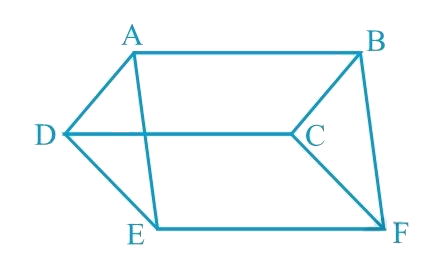
In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF)
Solution:
We can see that the sides of triangles ADE and BCF are also the opposite sides of the given parallelograms. Now, we can show both the triangles congruent by SSS congruency.
Also, we know that congruent triangles have equal areas.
It is given that ABCD is a parallelogram. We know that opposite sides of a parallelogram are equal.
∴ AD = BC ... (1)
Similarly, for parallelograms DCFE and ABFE, it can be said that DE = CF ... (2)
and, EA = FB ... (3)
In ΔADE and ΔBCF,
AD = BC [Using equation (1)]
DE = CF [Using equation (2)]
EA = FB [Using equation (3)]
∴ ΔADE ≅ ΔBCF (SSS congruence rule)
The SSS rule states that if three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.
∴ Area (ΔADE) = Area (ΔBCF)
☛ Check: Class 9 Maths NCERT Solutions Chapter 9
Video Solution:
In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF)
Maths NCERT Solutions Class 9 Chapter 9 Exercise 9.4 Question 3
Summary:
If ABCD, DCFE, and ABFE are parallelograms in the given figure, ar (ΔADE) = ar (ΔBCF) since ΔADE ≅ ΔBCF by SSS congruence.
☛ Related Questions:
- In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).[Hint: Join AC.]
- In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show thati) ar (BDE) =1/4 ar (ABC)ii) ar (BDE) = 1/2 ar (BAE)iii) ar (ABC) = 2 ar (BEC)iv) ar (BFE) = ar (AFD)v) ar (BFE) = 2 ar (FED)vi) ar (FED) = 1/8 ar (AFC)[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]
- Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC)[Hint: From A and C, draw perpendiculars to BD.]
- P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show thati) ar (PRQ) = 1/2 ar (ARC)ii) ar (RQC) = 3/8 ar (ABC)iii) ar (PBQ) = ar (ARC)
visual curriculum