In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:
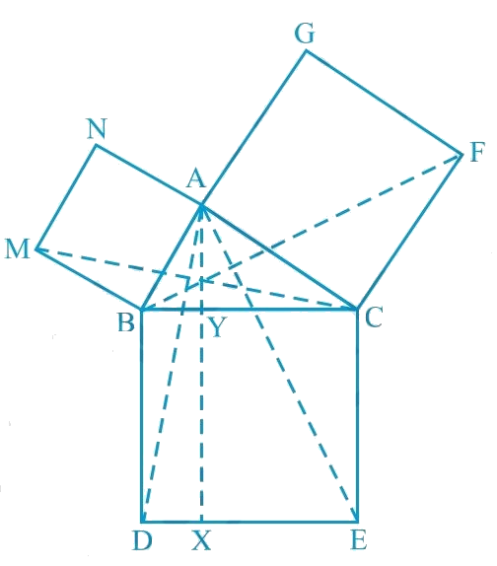
i) ΔMBC ≅ ΔABD
ii) ar (BYXD) = 2 ar (MBC)
iii) ar (BYXD) = ar (ABMN)
iv) ΔFCB ≅ ΔACE
v) ar (CYXE) = 2ar (FCB)
vi) ar (CYXE) = ar (ACFG)
vii) ar (BCED) = ar (ABMN) + ar (ACFG)
Solution:
We can use a suitable congruency rule to show the triangles congruent. Also, we can use some theorem or properties like triangle and parallelogram on the same base and between the same parallels. The Triangle area will be half of the parallelogram area.
i) We know that each angle of a square is 90°.
Hence,
∠ABM = ∠DBC = 90o
∴ ∠ABM + ∠ABC = ∠DBC + ∠ABC
∴ ∠MBC = ∠ABD
In ΔMBC and ΔABD,
∠MBC = ∠ABD (Proved above)
MB = AB (Sides of square ABMN)
BC = BD (Sides of square BCED)
∴ ΔMBC ≅ ΔABD (By SAS congruence rule)
ii) We have ΔMBC ≅ ΔABD
∴ ar (ΔMBC) = ar (ΔABD)...(1)
It is given that AX ⊥ DE and BD ⊥ DE (Adjacent sides of square BDEC)
∴ BD|| AX (Two lines perpendicular to the same line are parallel to each other)
∆ABD and parallelogram BYXD are on the same base BD and between the same parallels BD and AX.
Area (∆BYXD) = 2 Area (∆MBC) [Using equation (1)] ... (2)
iii) ΔMBC and parallelogram ABMN lie on the same base MB and between the same parallels MB and NC.
2 ar (ΔMBC) = ar (ABMN)
ar (BYXD) = ar (ABMN) [Using equation (2)]...(3)
iv) We know that each angle of a square is 90°.
∴ ∠FCA = ∠BCE = 90o
∴ ∠FCA + ∠ACB = ∠BCE + ∠ACB
Adding ∠ACB on both the sides
∴ ∠FCB = ∠ACE
In ΔFCB and ΔACE,
FC = AC (Sides of square ACFG)
CB = CE (Sides of square BCED)
ΔFCB ≅ ΔACE (SAS congruence rule)
SAS Congruence Rule - If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle, then the triangles are congruent.
v) It is given that AX ^ DE and CE ^ DE (Adjacent sides of square BDEC)
Hence, CE || AX (Two lines perpendicular to the same line are parallel to each other) Consider ∆ACE and parallelogram CYXE
DACE and parallelogram CYXE are on the same base CE and between the same parallels CE and AX.
∴ ar (ΔCYXE) = 2 ar (ΔACE)....... (4)
We had proved that
\ΔFCB ≅ ΔACE
ar (ΔFCB) ≅ ar (ΔACE)...........(5)
On comparing equations (4) and (5), we obtain
ar (CYXE) = 2 ar (ΔFCB)....(6)
vi) Consider ∆FCB and parallelogram ACFG
ΔFCBand parallelogram ACFG are lying on the same base CF and between the same parallels CF and BG.
∴ ar (ACFG) = 2 ar (ΔFCB)
∴ ar (ACFG) = ar (CYXE) [Using equation (6)]...(7)
vii) From the figure, it is evident that
ar (BCED) = ar (BYXD) + ar (CYXE)
∴ ar (BCED) = ar (ABMN) + ar (ACFG) [Using equations (3) and (7)]
☛ Check: NCERT Solutions Class 9 Maths Chapter 9
Video Solution:
In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that: i) ΔMBC ≅ ΔABD ii) ar (BYXD) = 2ar (MBC) iii) ar (BYXD) = ar (ABMN) iv) ΔFCB ≅ ΔACE v) ar (CYXE) = 2ar (FCB) vi) ar (CYXE) = ar (ACFG) vii) ar (BCED) = ar (ABMN) + ar (ACFG) Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in class X.
Maths NCERT Solutions Class 9 Chapter 9 Exercise 9.4 Question 8
Summary:
If ABC is a right triangle right angled at A and BCED, ACFG, and ABMN are squares on the sides BC, CA, and AB respectively, and line segment AX⊥DE meets BC at Y, then ΔMBC ≅ ΔABD, ar (BYXD) = 2 ar (MBC), ar (BYXD) = 2 ar (ABMN), ΔFCB ≅ ΔACE, ar (CYXE) = 2 ar (FCB), ar (CYXE) = ar (ACFG), and ar (BCED) = {ar (ABMN) + ar (ACFG)}.
☛ Related Questions:
- In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).[Hint: Join AC.]
- In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show thati) ar (BDE) =1/4 ar (ABC)ii) ar (BDE) = 1/2 ar (BAE)iii) ar (ABC) = 2 ar (BEC)iv) ar (BFE) = ar (AFD)v) ar (BFE) = 2 ar (FED)vi) ar (FED) = 1/8 ar (AFC)[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]
- Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC)[Hint: From A and C, draw perpendiculars to BD.]
- P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show thati) ar (PRQ) = 1/2 ar (ARC)ii) ar (RQC) = 3/8 ar (ABC)iii) ar (PBQ) = ar (ARC)
visual curriculum