In Fig.9.23, E is any point on median AD of a ∆ ABC. Show that ar  (ABE) = ar (ACE).

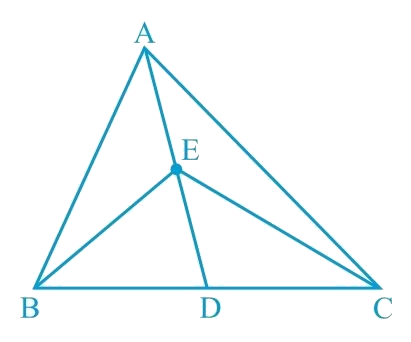
Solution:

We know that the median divides a triangle into two triangles of equal areas. AD is the median for triangle ABC and ED is the median of triangle EBC. 

Since AD is the median of ΔABC. Therefore, it will divide ∆ABC into two triangles of equal areas.

Hence, Area (ΔABD) = Area (ΔACD)  ... (1)

Similarly, ED is the median of ΔEBC.

Hence, Area (ΔEBD) = Area (ΔECD)  ... (2)

Substract equation (2) from equation (1), we obtain

ar (ΔABD) - ar (ΔEBD) = ar (ΔACD) - ar (ΔECD)

Area (ΔABE) = Area (ΔACE)

☛ Check: NCERT Solutions Class 9 Maths Chapter 9

Video Solution:

In Fig.9.23, E is any point on median AD of a ∆ ABC. Show that ar  (ABE) = ar (ACE).
 

Maths NCERT Solutions Class 9 - Chapter 9 Exercise 9.3 Question 1:

Summary:

If E is any point on the median AD of triangle ABC, then Area of (ABE) = Area of (ACE).

☛ Related Questions:

• In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 1/4 ar(ABC).
• Show that the diagonals of a parallelogram divide it into four triangles of equal area.
• In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar(ABC) = ar (ABD).
• D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that: i) BDEF is a parallelogram. ii) ar (DEF) = 1/4 ar (ABC) iii) ar (BDEF) = 1/2 ar (ABC)