LCM of 60 and 70
LCM of 60 and 70 is the smallest number among all common multiples of 60 and 70. The first few multiples of 60 and 70 are (60, 120, 180, 240, 300, 360, . . . ) and (70, 140, 210, 280, 350, 420, 490, . . . ) respectively. There are 3 commonly used methods to find LCM of 60 and 70 - by listing multiples, by division method, and by prime factorization.
| 1. | LCM of 60 and 70 |
| 2. | List of Methods |
| 3. | Solved Examples |
| 4. | FAQs |
What is the LCM of 60 and 70?
Answer: LCM of 60 and 70 is 420.

Explanation:
The LCM of two non-zero integers, x(60) and y(70), is the smallest positive integer m(420) that is divisible by both x(60) and y(70) without any remainder.
Methods to Find LCM of 60 and 70
The methods to find the LCM of 60 and 70 are explained below.
- By Prime Factorization Method
- By Division Method
- By Listing Multiples
LCM of 60 and 70 by Prime Factorization
Prime factorization of 60 and 70 is (2 × 2 × 3 × 5) = 22 × 31 × 51 and (2 × 5 × 7) = 21 × 51 × 71 respectively. LCM of 60 and 70 can be obtained by multiplying prime factors raised to their respective highest power, i.e. 22 × 31 × 51 × 71 = 420.
Hence, the LCM of 60 and 70 by prime factorization is 420.
LCM of 60 and 70 by Division Method
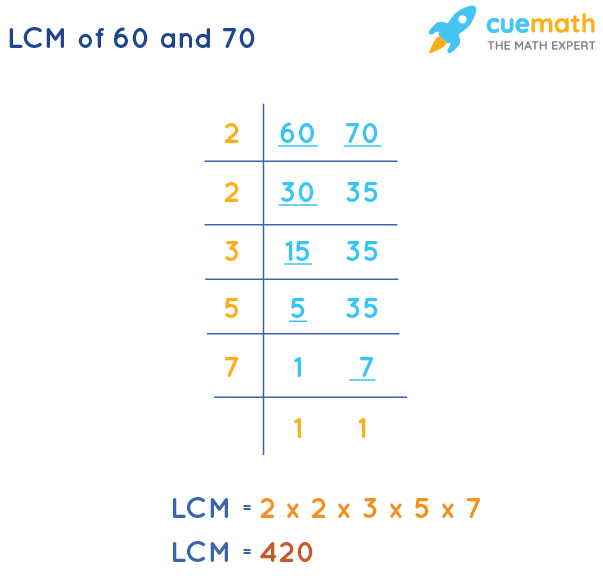
To calculate the LCM of 60 and 70 by the division method, we will divide the numbers(60, 70) by their prime factors (preferably common). The product of these divisors gives the LCM of 60 and 70.
- Step 1: Find the smallest prime number that is a factor of at least one of the numbers, 60 and 70. Write this prime number(2) on the left of the given numbers(60 and 70), separated as per the ladder arrangement.
- Step 2: If any of the given numbers (60, 70) is a multiple of 2, divide it by 2 and write the quotient below it. Bring down any number that is not divisible by the prime number.
- Step 3: Continue the steps until only 1s are left in the last row.
The LCM of 60 and 70 is the product of all prime numbers on the left, i.e. LCM(60, 70) by division method = 2 × 2 × 3 × 5 × 7 = 420.
LCM of 60 and 70 by Listing Multiples
To calculate the LCM of 60 and 70 by listing out the common multiples, we can follow the given below steps:
- Step 1: List a few multiples of 60 (60, 120, 180, 240, 300, 360, . . . ) and 70 (70, 140, 210, 280, 350, 420, 490, . . . . )
- Step 2: The common multiples from the multiples of 60 and 70 are 420, 840, . . .
- Step 3: The smallest common multiple of 60 and 70 is 420.
∴ The least common multiple of 60 and 70 = 420.
☛ Also Check:
- LCM of 72 and 108 - 216
- LCM of 13 and 91 - 91
- LCM of 12, 45 and 75 - 900
- LCM of 34 and 51 - 102
- LCM of 40, 42 and 45 - 2520
- LCM of 56 and 70 - 280
- LCM of 16, 20 and 24 - 240
LCM of 60 and 70 Examples
-
Example 1: Find the smallest number that is divisible by 60 and 70 exactly.
Solution:
The smallest number that is divisible by 60 and 70 exactly is their LCM.
⇒ Multiples of 60 and 70:- Multiples of 60 = 60, 120, 180, 240, 300, 360, 420, . . . .
- Multiples of 70 = 70, 140, 210, 280, 350, 420, 490, . . . .
Therefore, the LCM of 60 and 70 is 420.
-
Example 2: The product of two numbers is 4200. If their GCD is 10, what is their LCM?
Solution:
Given: GCD = 10
product of numbers = 4200
∵ LCM × GCD = product of numbers
⇒ LCM = Product/GCD = 4200/10
Therefore, the LCM is 420.
The probable combination for the given case is LCM(60, 70) = 420. -
Example 3: Verify the relationship between GCF and LCM of 60 and 70.
Solution:
The relation between GCF and LCM of 60 and 70 is given as,
LCM(60, 70) × GCF(60, 70) = Product of 60, 70
Prime factorization of 60 and 70 is given as, 60 = (2 × 2 × 3 × 5) = 22 × 31 × 51 and 70 = (2 × 5 × 7) = 21 × 51 × 71
LCM(60, 70) = 420
GCF(60, 70) = 10
LHS = LCM(60, 70) × GCF(60, 70) = 420 × 10 = 4200
RHS = Product of 60, 70 = 60 × 70 = 4200
⇒ LHS = RHS = 4200
Hence, verified.

FAQs on LCM of 60 and 70
What is the LCM of 60 and 70?
The LCM of 60 and 70 is 420. To find the least common multiple of 60 and 70, we need to find the multiples of 60 and 70 (multiples of 60 = 60, 120, 180, 240 . . . . 420; multiples of 70 = 70, 140, 210, 280 . . . . 420) and choose the smallest multiple that is exactly divisible by 60 and 70, i.e., 420.
Which of the following is the LCM of 60 and 70? 12, 28, 420, 10
The value of LCM of 60, 70 is the smallest common multiple of 60 and 70. The number satisfying the given condition is 420.
If the LCM of 70 and 60 is 420, Find its GCF.
LCM(70, 60) × GCF(70, 60) = 70 × 60
Since the LCM of 70 and 60 = 420
⇒ 420 × GCF(70, 60) = 4200
Therefore, the greatest common factor = 4200/420 = 10.
What is the Least Perfect Square Divisible by 60 and 70?
The least number divisible by 60 and 70 = LCM(60, 70)
LCM of 60 and 70 = 2 × 2 × 3 × 5 × 7 [Incomplete pair(s): 3, 5, 7]
⇒ Least perfect square divisible by each 60 and 70 = LCM(60, 70) × 3 × 5 × 7 = 44100 [Square root of 44100 = √44100 = ±210]
Therefore, 44100 is the required number.
How to Find the LCM of 60 and 70 by Prime Factorization?
To find the LCM of 60 and 70 using prime factorization, we will find the prime factors, (60 = 2 × 2 × 3 × 5) and (70 = 2 × 5 × 7). LCM of 60 and 70 is the product of prime factors raised to their respective highest exponent among the numbers 60 and 70.
⇒ LCM of 60, 70 = 22 × 31 × 51 × 71 = 420.
visual curriculum