Sum of Integers Formula

Before learning the sum of integers formula, let us recall what are integers. Numbers without fractional or decimal components are integers. The sum of integers can be calculated by doing simple mathematics when the numbers to be added are less. But if it is required to add many consecutive integers at a time, we use the sum of integers formula. It simplifies our calculations involved and minimizes our time of addition. 

What Is the Sum of Integers Formula?

The sum of integers formula is nothing but the sum of n terms of an arithmetic sequence. The sum of integers formula is:

Sum of Integers Formula:

S = n(a + l)/2

where,

• S = sum of the consecutive integers
• n = number of integers
• a = first term
• l = last term

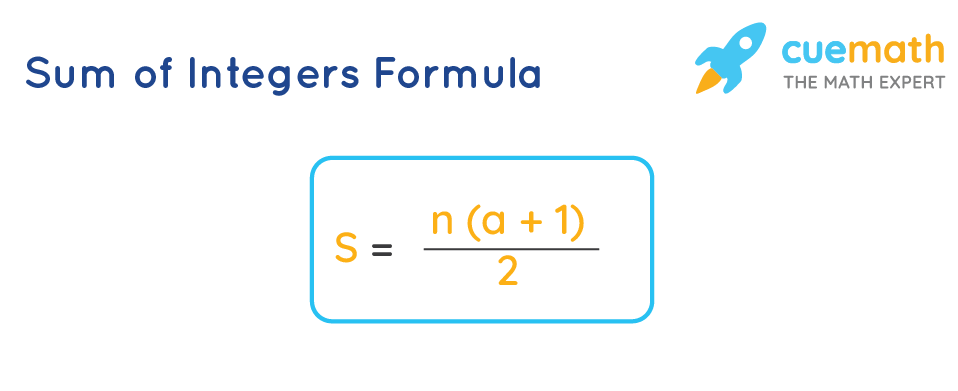
Also, the sum of first 'n' positive integers can be calculated as, 

Sum of first n positive integers = n(n + 1)/2, where n is the total number of integers.

Let us see the applications of the sum of integers formula along with a few solved examples.

Examples Using Sum of Integers Formula

Example 1: Find the sum of integers from 1 to 1000.

Solution:   

To find: To find: Sum of integers from 1 to 1000.
Given,
n = 1000
a = 1
l = 1000

Using sum of integers Formula,

S = n(a + l)/2

S = 1000(1+1000)/2
S = 1000(1001)/2
S = (1001000)/2
S = 500500

Answer: Sum of integers from 1 to 1000 is 500500.

Example 2: Find the sum of integers -3, -2, -1, 0, 1, 2, 3, 4.

Solution: 

To find: Sum of integers from -3 to 4.
Given:
n = 8
a = -3
l = 4              

Using sum of integers formula,

S = n(a + l)/2

S = 8(-3 + 4)/2
S = 8(1)/2
S = 4

Answer: Sum of integers from -3 to 4 is 4.