Derivative of Cos Inverse (Arccos)
The derivative of cos inverse is the negative of the derivative of sin inverse. Derivative of cos inverse x gives the rate of change of the inverse trigonometric function arccos x and is given by d(cos-1x)/dx = -1/√(1 - x2), where -1 < x < 1. Derivative of cos inverse is the same as the derivative of arccos which is mathematically written as d(arccos)/dx = -1/√(1 - x2), where -1 < x < 1. Derivative of arccos can be calculated by the first principle of differentiation.
In this article, we will determine the derivative of cos inverse and prove that the derivative of arccos is -1/√(1 - x2) using various methods of differentiation with the help of some solved examples for a better understanding.
What is Derivative of Cos Inverse?
The derivative of cos inverse x is given by -1/√(1 - x2), where -1 < x < 1, which is negative of the derivative of sin inverse x. Mathematically, the derivative of arccos is written as d(cos-1x)/dx = d(arccos)/dx = -1/√(1 - x2). The derivative of cos inverse can be determined by implicit differentiation. The derivative of a function represents the rate of change of the function at some point. Since the derivative of cos inverse x is -1/√(1-x2), therefore the graph of the derivative of arccos will be the graph of -1/√(1-x2).
Derivative of Cos Inverse Formula
An easy way to memorize the formula for the derivative of cos inverse x is that it is the negative of the derivative of sin inverse x. The derivative of arccos gives the slope function of the inverse trigonometric function cos inverse x as the derivative of a function represents the slope of the function at a point of contact. Now that we know the derivative of arccos, let us write the formula for the derivative of cos inverse mathematically, which is given by d(cos-1x)/dx = -1/√(1 - x2), where -1 < x < 1.
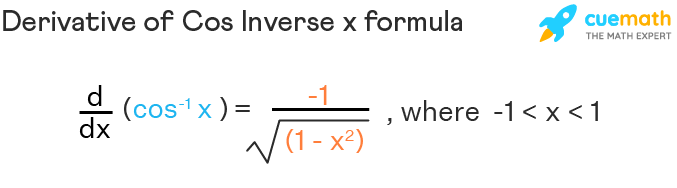
Derivative of Cos Inverse By First Principle
Since we know that the derivative of cos inverse x is -1/√(1 - x2), where -1 < x < 1, we will prove it using the definition of limits, that is, the first principle of differentiation. We will use different formulas of trigonometry, limits and differentiation which are given below:
- \(f'(x)=\lim_{h\rightarrow 0}\dfrac{f(x+h)-f(x)}{h}\)
- cos-1x + sin-1x = π/2
- d(sin-1x)/dx = \(\lim_{h\rightarrow 0}\dfrac{sin^{-1}(x+h)-sin^{-1}x}{h} = \dfrac{1}{\sqrt{1-x^2}}\)
\(\begin{align}\frac{\mathrm{d} \cos^{-1}x}{\mathrm{d} x} &=\lim_{h\rightarrow 0}\dfrac{ \cos^{-1}(x+h)- \cos^{-1}x}{h}\\&=\lim_{h\rightarrow 0}\dfrac{\frac{\pi}{2}-\sin^{-1}(x+h)-\frac{\pi}{2}+\sin^{-1}x}{h}\\&=\lim_{h\rightarrow 0}\dfrac{-\sin^{-1}(x+h)+\sin^{-1}x}{h}\\&=-\lim_{h\rightarrow 0}\dfrac{\sin^{-1}(x+h)-\sin^{-1}x}{h}\\&=-\frac{\mathrm{d} \sin^{-1}x}{\mathrm{d} x} \\&=-\dfrac{1}{\sqrt{1-x^2}}\end{align}\)
Hence we have determined the derivative of arccos using the first principle of differentiation.
Derivative of Arccos By Implicit Differentiation
Now, we will find the derivative of arccos, that is, cos-1x using implicit differentiation.
Let us assume y = cos-1x. Then, cos y = x
Differentiate cos y = x implicitly with respect to x.
(-sin y) dy/dx = 1 ----- (i)
By trigonometric identity, we know that
sin2y + cos2y = 1
⇒ sin2y + x2 = 1
⇒ sin2y = 1 – x2
⇒ sin y = √(1 − x2)
Substituting the above value in (i), we get
−√(1 − x2) dy/dx = 1
⇒ dy/dx = –1/√(1 − x2), -1 < x < 1
Hence we have proved the derivative cos inverse using implicit differentiation.
Derivative of Cos Inverse x With Respect To Sin Inverse x
To determine the derivative of cos inverse x with respect to sin inverse x, we will use the derivative of cos inverse x and the derivative of sin inverse x. We have
- d(cos-1x)/dx = -1/√(1 - x2)
- d(sin-1x)/dx = 1/√(1 - x2) ⇒ dx/d(sin-1x) = √(1 - x2)
We need to determine the value of d(cos-1x)/d(sin-1x).
d(cos-1x)/d(sin-1x) = [d(cos-1x)/dx]/[d(sin-1x)/dx]
= [d(cos-1x)/dx] × dx/d(sin-1x)
= [-1/√(1 - x2)] × √(1 - x2)
= -1
Hence the derivative of cos inverse x with respect to sin inverse x is -1.
Important Notes on Derivative of Cos Inverse
- The derivative of cos inverse is the negative of the derivative of sin inverse.
- The domain of the derivative of arccos is (-1,1).
- The derivative of cos inverse x is given by d(cos-1x)/dx = -1/√(1 - x2), where -1 < x < 1.
Related Topics on Derivative of Cos Inverse
Examples Using Derivative of Cos Inverse
-
Example 1: Determine the derivative of cos inverse 2x using the derivative of cos inverse x formula.
Solution: To determine the derivative of cos inverse 2x using the derivative of cos inverse x formula, we will apply chain rule.
d(cos-12x)/dx = d(cos-12x)/d(2x) × d(2x)/dx
= -1/√(1 - (2x)2) × 2
= -2/√(1 - 4x2)
Answer: Hence derivative of cos inverse 2x is -2/√(1 - 4x2).
-
Example 2: Find the derivative of cos inverse x + sin inverse x.
Solution: We know that the derivative of cos inverse x is -1/√(1 - x2) and the derivative of sin inverse x is 1/√(1 - x2). Also, the derivative of sum of two functions is equal to the sum of the derivatives of the two functions, therefore we have
d(cos-1x + sin-1x)/dx = d(cos-1x)/dx + d(sin-1x)/dx
= -1/√(1 - x2) + 1/√(1 - x2)
= 0
Answer: The derivative of cos inverse x + sin inverse x is 0.

FAQs on Derivative of Cos Inverse
What is Derivative of Cos Inverse in Trigonometry?
The derivative of cos inverse is the negative of the derivative of sin inverse, given by d(cos-1x)/dx = -1/√(1 - x2), where -1 < x < 1
How to Find the Derivative of Cos Inverse?
The derivative of cos inverse x can be determined using different methods including the first principle of differentiation, substitution method, implicit differentiation, etc.
What is the Derivative of Cos Inverse Root x?
The derivative of cos inverse root x is d(cos-1√x)/dx = -1/[2√(x(1 - x))].
What is the Derivative of Arccos Formula?
The formula for the derivative of cos inverse mathematically is given by d(cos-1x)/dx = -1/√(1 - x2), where -1 < x < 1.
What is the Derivative of Cos Inverse x With Respect to Sin Inverse x?
The derivative of cos inverse x with respect to sin inverse x is -1.
visual curriculum