A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
LearnPracticeDownload

Linear, Quadratic and Cubic Polynomials

Polynomials are one of the significant concepts of mathematics, and so are the types of polynomials that are determined by the degree of polynomials, which further determines the maximum number of solutions a function could have and the number of times a function will cross the x-axis when graphed. Let's learn in detail about linear, quadratic, and cubic polynomials.

1. What are Linear, Quadratic and Cubic Polynomials?
2. Linear Polynomials
3. Quadratic Polynomials
4. Cubic Polynomials

What are Linear, Quadratic and Cubic Polynomials?

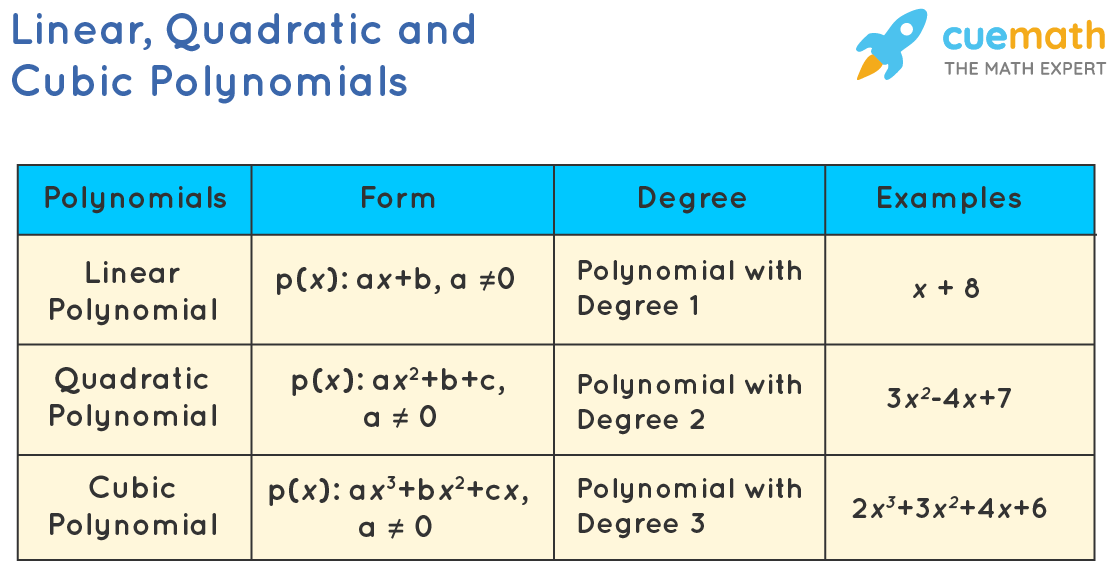
Each of the polynomials has a specific degree and based on that they have been assigned a specific name and are thus referred to as different types of polynomials. Let's know about linear, quadratic, and cubic polynomials.

Linear, Quadratic and Cubic Polynomials

Linear Polynomials

A linear polynomial is a polynomial of degree one, i.e., the highestexponent of the variable is one, defined by an equation of the form: p(x): ax + b, a≠0.

Given below are a few examples of linear polynomials:

  • p(x): 2x + 3
  • q(y): πy + √2
  • r(z): z + √5
  • s(x): −7x

We note that a linear polynomial in one variable can have at the most two terms. The constraint that a should not be equal to 0 is required because if a is 0, then this becomes a constant polynomial.

Example: Is 1/x a linear polynomial?

Solution: In general form, we can write it as 1/x-1 + 0. Clearly, the degree of this polynomial is not one, it is not a linear polynomial.

Quadratic Polynomials

A quadratic polynomial is a polynomial of degree two,i.e., the highest exponent of the variable is two. In general, a quadratic polynomial will be of the form: p(x): ax2 + bx + c, a≠0

Given below are a few examples of quadratic polynomials:

  • p(x): 3x2 + 2x + 1
  • q(y): y2 − 1
  • r(z): √2z2

We observe that a quadratic polynomial can have at the most three terms. The constraint that a should not be equal to 0 is required because if a is 0, then this becomes a linear polynomial.

Example: Which of the following are quadratic polynomials?

  1. y2 + √2
  2. x + 2/x
  3. πx2/2 + x

Solution: In (1) and (3), the degree of polynomial is two. But In (2), the exponent of term 2/x is not a whole number. So, (1) and (3) are quadratic polynomials, and (2) are not even polynomial.

Cubic Polynomials

A cubic polynomial is a polynomial of degree three, i.e., the highest exponent of the variable is three. A cubic polynomial, in general, will be of the form p(x): ax3 + bx2 + cx + d, a≠0

Given below are a few examples of cubic polynomials:

  • p(x): x3 − 6x2 + 11x − 6
  • q(y): 27y3 − 1
  • r(z): πz3 + (√2)10

We observe that a cubic polynomial can have at the most four terms. Once again, the constraint that a should not be equal to 0 is required because if a is 0, then this becomes a quadratic rather than a cubic polynomial.

Tips and Tricks

  • After converting any expression into the general form, if the exponent of the variable in any term is not a whole number, then it's not a polynomial either.
  • For any polynomial of positive order, there are a maximum number of zeros equal to its order.

Important Notes

  • Why do we use the adjective linear? It turns out that when we draw the graph corresponding to a linear polynomial, we will get a straight line – hence the name linear.
  • A polynomial of degree n will have n number of zeros or roots.
  • A polynomial can have any number of terms, but never infinite.
  • Zeros correspond to expressions, and roots correspond to equations.
  • A linear polynomial has only one zero.
  • A quadratic polynomial can have at most two zeros, whereas a cubic polynomial can have at most 3 zeros.

Related Topics

Examples on Linear, Quadratic, and Cubic Polynomials

  1. Example 1: Classify the given polynomials as linear, quadratic or cubic polynomials:

    p(x): 5x2 + 6x + 1
    p(x): 2x + 3
    q(z): z2 − 1
    r(z): z2 + (√2)9
    r(z): √5z2
    s(x): 10x
    p(y): y3 − 6y2 + 11y − 6
    q(y): 81y3 − 1
    r(z): z + 3

    Solution:

    The given polynomials can be classified as follows:

    Linear Polynomials Quadratic Polynomials Cubic Polynomials

    p(x): 2x + 3

    r(z): z + 3

    s(x): 10x

    p(x): 5x2 + 6x + 1

    q(z): z2 − 1

    r(z): √5z2

    p(y): y3 − 6y2 + 11y − 6

    q(y): 81y3 − 1

    r(z): z2 + (√2)9

     

  2. Example 2: Verify whether the 1 and 0 are the zeros of the given polynomials:

    27x3 − 1
    x + 2
    2x2 + x - 3

    Solution:

    p(x) = 27x3 − 1, p(0) = 27(0)3 - 1 = - 1, p(1) = 27(1)3 - 1 = 26. Therefore, 0 and 1 are not the zeros of the polynomial 27x3 − 1
    p(x) = x + 2, p(0) = (0) + 2 = 2, p(1) = (1) + 2 = 3. Therefore, 0 and 1 are not the zeros of the polynomial x + 2
    p(x) = 2x2 + x - 3, p(0) = 2(0)2 + (0) - 3 = -3, p(1) = 2(1)2 + (1) - 3 = 0. Therefore, 0 is the zero of the polynomial 2x2 + x - 3 but 1 is not.

     

Show More >

go to slidego to slide

Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

 

FAQs on Linear, Quadratic, and Cubic Polynomials

How do you know if a Polynomial is Linear?

A polynomial of degree one is called the linear polynomial. That is, the highest exponent of the variable is one, then the polynomial is said to be a linear polynomial.

How to Classify Linear, Quadratic, and Cubic Polynomials?

Linear, quadratic and cubic polynomials can be classified on the basis of their degrees.

  • A polynomial of degree one is a linear polynomial. For example, 5x + 3
  • A polynomial of degree two is a quadratic polynomial. For example, 2x2 + x + 5
  • A polynomial of degree three is a cubic polynomial. For example, y3 − 6y2 + 11y − 6

How to Solve Cubic Polynomials?

The most commonly used strategy for solving a cubic equation is

  • Step 1: Reduce a cubic polynomial to a quadratic equation.
  • Step 2: Solve the quadratic equation using the quadratic formula.

What is the Equation for Cubic Polynomials?

A cubic equation is an algebraic equation of degree three and is of the form ax3 + bx2 + cx + d = 0, where a, b and c are the coefficients and d is the constant.

How to Factor Quadratic Polynomials?

Factorization of cubic polynomials can be done by the following methods:

  • Common Factor Method: In this method, we have to look at all the terms and determine the common terms. If there is a common term in the equation, we will factor it out for the polynomial.
  • Sum of Difference Method: The sum and the difference of two terms is most likely used when the two factors match exactly, except one term involves addition and the other is a difference.
  • Product Sum Method: In the product sum method for factoring polynomials, we use trinomials (ax2+bx+c), where the value of a is 1. This method is probably used the most for factoring polynomials.
  • Factor by Grouping Method: Factor by grouping means that we have to group all the terms with common factors before factoring.
  • Perfect Square Trinomials Method: The method of converting any trinomial into the perfect square is known as the perfect square trinomial method.
Download FREE Study Materials
Download Polynomials Worksheets
Math worksheets and
visual curriculum