Polar Coordinates
Geographical positioning makes use of the angles from a reference axis to locate specific points on the earth.

The polar coordinate system is quite similar to this positioning system.
The polar coordinate system is a two-dimensional coordinate system in which the location of each point could be traced using two references:
1. Its distance from a reference line.
2. Its angle from a reference direction.
Learn about polar coordinates grapher, polar coordinates formula, and polar coordinates examples in the concept of polar coordinates.Check out the interactive polar coordinates calculator to know more about the lesson and try your hand at solving a few interesting practice questions at the end of the page.
Lesson Plan
What Are Polar Coordinates?
A coordinate system uses unique numbers to determine the position of a point or any geometric element. Such a position indicating numbers are called coordinates.
Two commonly used coordinate systems are:
1. The Cartesian coordinate system
The Cartesian coordinate system specifies each point uniquely in a plane by a set of numerical coordinates. The distances are measured from two fixed perpendicular oriented lines (X-axis and Y-axis) measured in the same unit of length. It is also called a rectangular coordinate system.

2. The polar coordinate system
It is a two-dimensional coordinate system in which each point on a plane has a unique distance from a reference point and a specific angle from a reference direction.
By using polar coordinates we mark a point by how far away and at what angle it is.

Here, the point P is at a distance '\( \text r \)' from the origin (0) and is at an angle of \( θ \) from the reference axis i.e., the \( x\)-axis.
The origin is called the pole, and the \( x\)-axis is termed as the polar axis.

The grid pattern for both the coordinate systems is presented below.

The polar coordinate plane is a series of concentric circles around a central point of reference, called the pole. Each circle represents one radius unit, and lines denoting angles in radians are seen.
How to Plot Points Using Polar Coordinates?
The general form for writing polar coordinates is P (\(\text r, \theta \))
The radial coordinate is often denoted by \(\text {r} \), and the angular coordinate by \(\theta\).
Angles in polar coordinates are expressed in either degrees or radians.
\[360^{\circ} = 2 \pi\,\, \text {radians}\]
A diagram for interconversion of radians and degrees is presented below for quick reference.

Example: Plot the points M \((2, \dfrac \pi {2})\) and N\((3, \dfrac {3\pi} {4})\) on a polar coordinate plane. Can you also identify the polar coordinate of the point C?
Solution: The points M and N can be plotted on a polar coordinate plane as given below.

The polar coordinates of point C are \((2, \dfrac {7\pi}{4})\).
What Are the Formulas for Converting Between Polar and Cartesian Coordinates?
The formulas for the conversion of polar coordinates into Cartesian coordinates and vice-versa involve trigonometric functions.
Here are the formulas:
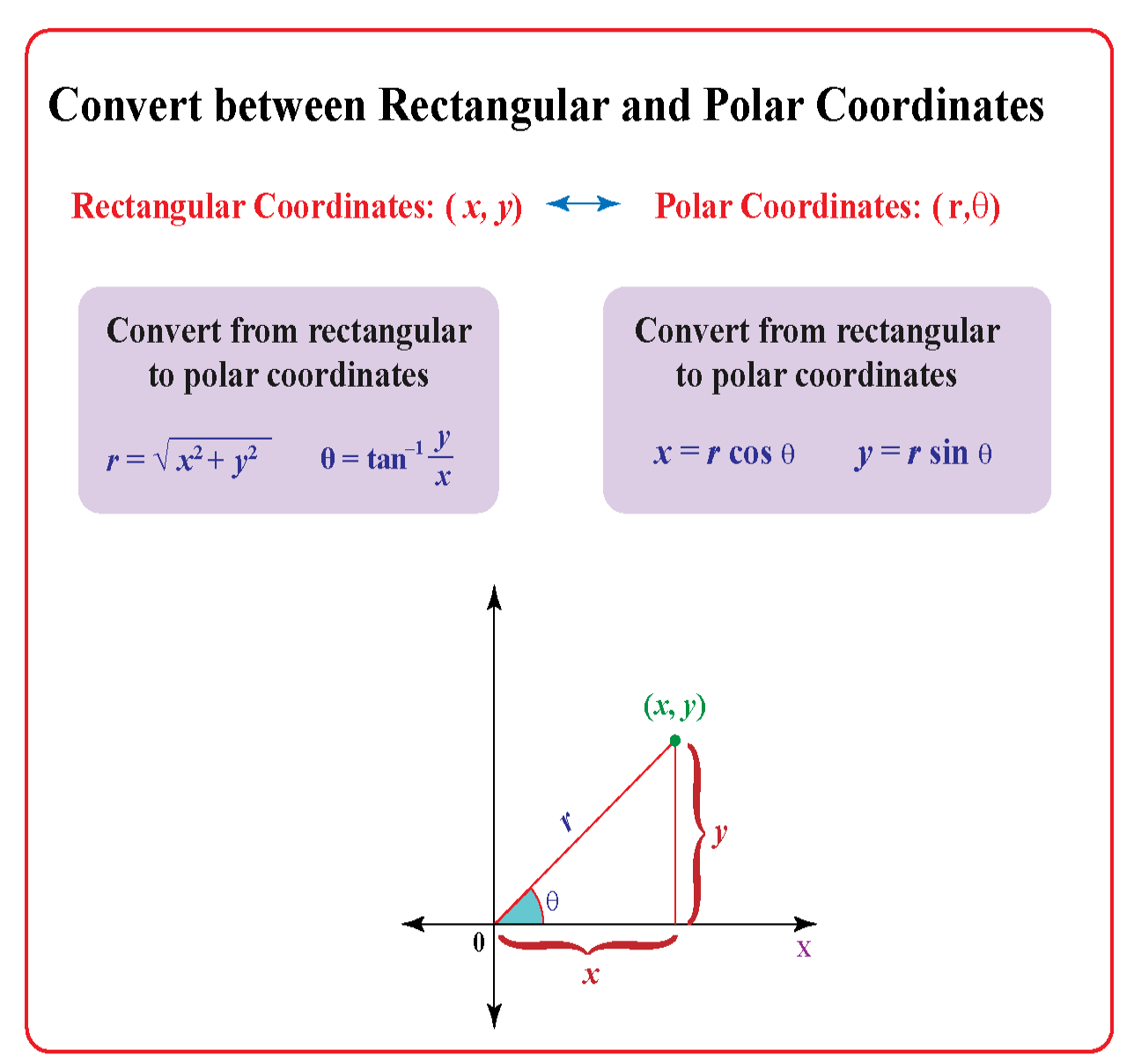
Let us explore the above formulas more.
How to Convert Polar Coordinates into Cartesian Coordinates?
We can convert polar coordinates into Cartesian coordinates \( (x, y ) \) by using the trigonometric functions \( \sin \)and \( \cos\).
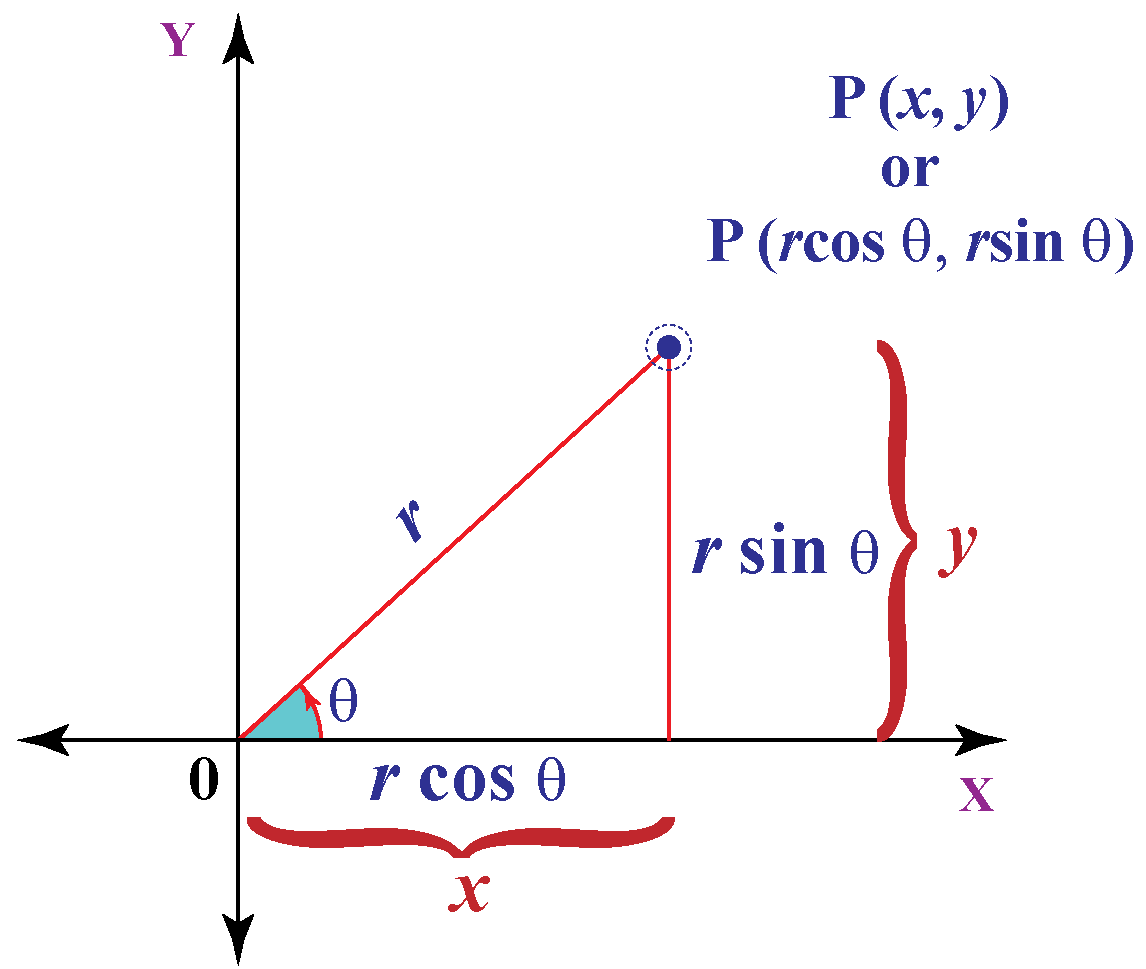
The above diagram illustrates the relationship between polar and Cartesian coordinates.
So, to convert from polar coordinates \((r , \theta)\) to Cartesian coordinates \( ( x, y) \) the formula is:
|
\(x = r \cos \theta \) \( y = r \sin \theta \) |
Example: What will be Cartesian coordinates for polar coordinates (\(10, 30^{\circ}\))?
Solution: For \( x \) coordinate, we will use the cosine function
\[ x = r \times \cos θ \]
For \(y\) coordinate, we will use the sine function, \(y = r \times \sin θ \)
Putting \( r = 10 \)
\[\begin {align*}\cos 30 &= \dfrac{\sqrt{3}}{2}\\
x &=10 \times \sqrt3 / 2\\
x &=5 \sqrt{3} \\
x &=5 \times 1.732 \\
x &=8.66
\end{align*}\]
For \( y \) we will use sine function
\[\begin {align*}\sin 30^{\circ} &= \dfrac12 \\
y &= r \times \sin \theta \\
y &= 10 \times \frac12 \\
y &= 5 \end{align*}\]
The polar coordinates \( (10 ,30^{\circ}) \) are almost exactly \( (8.66, 5) \) in Cartesian coordinates.
How to Convert Cartesian Coordinates into Polar Coordinates?
If we know the point in Cartesian coordinates \( (x, y )\) and if we want to know the polar coordinates we solve a right triangle with two known sides.
Example: What is (15, 8) in polar coordinates?

Using Pythagoras theorem to find the long side \(\text r\) (the hypotenuse) we get:
\[ \text {r}^2 = (15^2 + 8^2)\]
\[ \text {r} = \sqrt {(15^2 + 8^2)}\]
\[ \text {r} = \sqrt {(225 + 64)}\]
\[ \text {r} = \sqrt{(289)} = 17\]
Using the tangent function to find the angle:
\[ \text {tan} (θ ) = \dfrac {15}{8}\]
\[ \theta = \tan^{-1} \left( \dfrac {8}{15} \right) = 28.07^{\circ} \]
The point \((15,8)\) is \((17, 28.07^{\circ})\) in polar coordinates.
What is tan-1?
It is also termed as an inverse tangent function/ arctangent.
The functions of tangent and arctangent are inverse.
Tangent takes an angle and gives us a ratio, whereas, inverse tangent takes a ratio like \( \dfrac 8{15} \) and gives us an angle.
Thus, Cartesian coordinates can be converted into polar coordinates by using the below-given formula:

The value of \(\tan^{-1} \left( \dfrac {y}{x} \right) \) for converting Cartesian coordinates to polar coordinates may need to be adjusted as per the quadrant in which the point lies:
Quadrant I: Use the calculated value
Quadrant II: Add \(180^{\circ}\) to the calculated value
Quadrant III: Add \(180^{\circ}\) to the calculated value
Quadrant IV: Add \(360^{\circ}\) to the calculated value
The above adjustments are done as the calculator can give an incorrect value of \(\tan^{-1}\).
Example: What will be the polar coordinates for the point (−4,-5)?

Solution:
P is in quadrant III.
The value of \(\text r\) can be calculated as
\[ \text {r} = \sqrt {(-4^2 + (-5)^2)}\]
\[ \text {r} = \sqrt {(16 + 25)}\]
\[ \text {r} = \sqrt{(41)} = 6.4\] Angular coordinate is
\[\theta= \tan^{-1}\left( \dfrac {-5}{−4} \right)\\
\theta = \tan^{-1}(1.25)\]
The calculator value for \(tan^{-1}(1.25)\) is \(51.34^{\circ}\)
For quadrant III we will addd \(180^{\circ}\) to the calculated value
\[\theta= 51.34^{\circ} + 180^{\circ} = 231.34^{\circ}\]
So the polar coordinates for the point \((−4, -5)\) are \((10.4, 231.34^{\circ})\)

-
The formula for converting rectangular coordinates \( ( x,y ) \) to polar coordinates \((r , \theta)\) is
\(\text r = \sqrt {(x)^2 + y^2)}\) and \(\theta = \tan^{-1}\left( \dfrac {y}{x} \right) \) -
The value of \(\text tan^{-1} \left( \dfrac {y}{x} \right)\ \) for converting Cartesian coordinates to polar coordinates may need to be adjusted as per the rules of the quadrant in which the point lies:
Quadrant I: Use the calculated value
Quadrant II: Add \(180^{\circ}\) to the calculated value
Quadrant III: Add \(180^{\circ}\) to the calculated value
Quadrant IV: Add \(360^{\circ}\) to the calculated value
Polar Coordinates Calculator
You can now easily convert Cartesian coordinates into polar coordinates and vice-versa with this calculator!

-
Are polar coordinates of a point unique?
-
If on a polar coordinate plane you are standing at point P\((2, \dfrac {5\pi} {4})\), what will be the shortest distance that you can take to reach \(y\)-axis?
Solved Examples
| Example 1 |
A planet revolves around a star. Considering the sun as the pole, what coordinate is represented by the red circular orbit of the planet? Angular or radial coordinate?

Solution
The red orbit represents the radial coordinate. The radial coordinate of the planet stays the same along the entire red orbit.
| Example 2 |
What are the polar coordinates of point P?

Solution
Point P is at a distance of \(7\) units from the origin at an angle of \(70^{\circ}\) from the reference \( x\)-axis.
|
\(\therefore\) Cartesian coordinates of point P are \((7, 70^{\circ})\) |
| Example 3 |
Can you determine the Cartesian coordinates of the point P?

Solution
\(r = 6\) and \(\theta = 60^{\circ}\)
So,
\(x = 6 \times \cos 60^{\circ} = 6 \times 0.5 = 3\)
\(y \!=\! 6 \times \sin 60^{\circ} \!=\! 6 \times 0.866 \!=\! 5.196 \!=\! 5.20\) (to two decimals)
So, Cartesian coordinates are P = \((3, 5.20)\) which is in Quadrant I.
|
\(\therefore\) Cartesian coordinates of point P are \( (3,5.20)\) |
| Example 4 |
Point \(\text M \) lies in the second quadrant. How would you locate this point using polar coordinates?

Solution
\(\text M\) = \((-2, 4)\)
\(\text M\) is in the fourth quadrant with \(x = -2\) and \(y = 4\)
We now know that
\[\begin{align*} \text {r} &= \sqrt {(x)^2 + y^2)}\\ \theta &= \tan^{-1}\left( \dfrac {y}{x} \right)\\ \text {r} &= \sqrt {(-2)^2 + 4^2}\\ \text {r} &= \sqrt {(4 + 16)}\\ \text {r} &= \sqrt {(20)}\\ \text {r} &= 4.47\end{align*}\]
Now,
\[\theta= \tan^{-1}\left( \dfrac {4}{−2} \right)\]
The calculator value for arctan\( (-2)\) is \(-63.43^{\circ}\)
Since point \(\text M\) lies in quadrant II, we will add \(180^{\circ}\) to the calculated value:
\[\theta = -63.43^{\circ} + 180^{\circ} = 116.57^{\circ}\]
|
\(\therefore\) Polar Coordinates for point \(\text M\) are \((4.47, 116.57^{\circ})\) |
| Example 5 |
The Cartesian coordinates of a certain point \(\text N\) are \((2, 6)\). How far is the point from the pole at an angle of about \(71.565^{\circ}\) (to three decimal places)?
Solution
To find the distance of point \(\text N\) from the origin, we will find the value of \(\text r\)
\[ \begin{align*}\text r &= \sqrt {(x^2 + y^2)}\\ \text r &= \sqrt {(2^2 + 6^2)}\\ \text r &= \sqrt {4 + 36}\\ \text r &= \sqrt {40} = 6.32\end{align*}\]
|
\(\therefore\) The point N is at a distance of \(6.32\) units from the pole |
Interactive Questions
Here are a few activities for you to practice. Select/Type your answer and click the "Check Answer" button to see the result.
Let's Summarize
The mini-lesson targeted the fascinating concept of polar coordinates. The math journey around polar coordinates starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever. Here lies the magic with Cuemath.
About Cuemath
At Cuemath, our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.
Frequently Asked Questions (FAQs)
1. What is the difference between rectangular and polar coordinates?
Rectangular coordinates, or cartesian coordinates, are expressed in the form \(x, y\). Polar coordinates, on the other hand, come in the form \((r, \theta\)).
Instead of using horizontal and vertical lines, we instead trace the angle \(\theta\), which is the direction, and then move out from the origin a certain distance \(\text r\).

2. Are polar coordinates unique?
Rectangular/ Cartesian coordinates are unique. Polar coordinates are not unique. Every point has infinitely polar coordinates that are not unique.
For example, the polar coordinates \((1, 315^{\circ})\), \((1, -45^{\circ})\) and \((1, 675^{\circ})\) all represent the same point.

One of the polar coordinates goes around a circle so by its nature it returns to the same point periodically (every \(2\pi\) radians) if you keep going in the same direction.
3. What is the polar equation?
A polar equation is an equation that describes a relation between \(\text r\) and \(\theta\), where \(\text r\) represents the distance from the pole (origin) to a point on a curve, and \(\theta\) represents the angle made by a point on a curve from the positive \(x\)-axis.