Introduction to 4th Grade Math Common Core Standards | Syllabus | Most Important Areas
There has been a growing need for a focused and coherent mathematics curriculum in the United States to improve achievement in mathematics. To address this need, the United States Common Core (USCC) Standards of mathematics for each grade have been laid out. The standards are described in detail to help educators plan appropriate pedagogical approaches to ensure achievement of outcomes. These standards are drawn from research in math education and models of best mathematical practices across the world.
Here are the highlights of the grade specific standards and ways to implement the same.
GRADE 4
In Grade 4, children extend their understanding of place value to large numbers. Consolidation of the four operations of whole numbers is one of the key focus areas in grade 4 with more emphasis on multiplication and division and their interrelationships. In addition to whole numbers, operations on fractions and their representation as decimals also gain prominence in Grade 4. Geometric reasoning is enhanced by having students analyze shapes and compare them using their attributes. Along with numbers and geometry, problem solving in measurement and interpretation of data is also dealt with in Grade 4.
In order to facilitate mastery of abstract concepts by young learners, Cuemath adopts a Concrete-Pictoria-Abstract (CPA) approach. The curriculum is aided with concrete models and visuals as much as possible to make the transition from concrete to abstract concepts seamless. In order to attain the grade level outcomes, the Cuemath curriculum exposes students to a lot of real world problem-solving and visual representations to introduce concepts.
The curriculum of Grade 4, spreads across 5 major domains.
- Operations and Algebraic Thinking
- Numbers and Operations in Base 10
- Numbers and Operations- Fractions
- Measurement and Data
- Geometry
Operations and Algebraic Thinking
According to USCC standards, algebraic thinking is one of the key focus areas in the later primary years to ensure a seamless transition from arithmetic to algebra in middle school. Difficulty in translating a situation to algebraic expression or equation can be attributed to limited comprehension of word problems on four operations in younger grades. While it is important to learn how to add, subtract, multiply or divide whole numbers, understanding the meaning of each of these operations and the various situations in which these are used are equally critical to building a strong foundation in algebra.
Let us understand this with an example from the Cuemath curriculum.

The obvious answer to this question is $20. However, many 4th or 5th grade students may come up with the answer as $9. The probable reason for this gap is that children misinterpret multiplicative comparison as additive comparison and hence add 4 and 5 to get 9 instead of multiplying 4 and 5.
In order to make the difference between additive comparison and multiplicative comparison very clear, USCC recommends interpretation of multiplication equation as a comparison situation (20 = 5 x 4 as 20 is 5 times as much as 4) and interpretation of comparison situation as a multiplication equation (20 is 5 times as much as 4 as 20 = 5 x 4) as important learning outcomes. Experience of word problems on multiplication and division involving ‘multiplicative comparison’ using visual representations is suggested by the Common Core.
USCC also emphasizes use of visual examples to establish that 5 times 4 and 4 times 5 are both equal to 20. This can be very well understood using the arrangement of objects in rectangular arrays as shown below.

The arrangement in the first figure represents 4 x 5 (4 rows of 5 counters each). The arrangement in the second figure that represents 5 x 4 (5 rows of 4 counters each) can be obtained just by rotation of the arrangement in figure 1. However, in either case the total number of counters is still 20. Thus, students can visualize how 4 x 5 and 5 x 4 lead to the same product.
Such visual representations help in understanding the Commutative Property of Multiplication. Internalizing these properties early, helps understand why xy and yx are like terms later when they learn algebra.
Numbers and Operations in Base 10
At the end of Grade 3, students develop an understanding of the place value system of numbers upto 9999. In Grade 4, the common core emphasizes generalizing the place value of multi-digit numbers. The idea that the value of a digit at a place shifts to its left when the number is multiplied by ten should be established through different problems.
Let us look at an example from the Cuemath curriculum.

In the above example, the students can observe how the place value of a digit at a place is ten times, its value at a place to its immediate right. This provides a generalized idea of the base ten numeration.
This understanding of place value aids in understanding the standard multiplication and division algorithm.
Here is an example from the Cuemath curriculum to show the multiplication of 1232 x 3.
1232 can be expressed by expanding the place values of each of its digits as 1000 + 200 + 30 + 2.
The product can be visually modeled as the sum of the areas of rectangles of length 1000 units, 200 units , 30 units and 2 units with the common width as 3 units as shown below.

The sum of the partial products of the place values of each digit of 1232 with 3, gives us the final product.
This model can be further connected to the standard algorithm as shown below.

It is important to establish the connection between the visual model and the standard algorithm. The use of such models serve as an aid to transition from concrete and pictorial models to abstract algorithms.
Numbers and Operations- Fractions
Many of us have struggled with fractions as kids and teachers of primary mathematics would certainly agree that it is one of the most difficult topics to teach. The representation of fraction as Numerator/Denominator adds to its complexity as two parts represent the same fractional number. Additionally, the approaches used to compare fractions or to perform operations on fractions are completely different from what is followed in case of whole numbers. Hence, it is imperative to help students understand the meaning of fractions first. To address these challenges, in Grade 4, Common Core recommends, use of visual models to represent equivalent fractions and perform fraction operations. Equivalent fraction is one of the main prerequisites to understand comparison of fractions and performing addition and subtraction of fractions with different denominators. Any gap in understanding this concept at this stage would impede learning the related topics later. However, in traditional classrooms equivalent fractions are taught by mere explanation of the procedure to generate them by multiplying or dividing the numerator and the denominator by the same number.
To understand the concept, it is very important to help students visualize why two fractions are equivalent before getting into the procedure to generate them.
The following example from the Cuemath curriculum shows how to establish a connection between the visual model of equivalent fractions and the procedure to generate them.
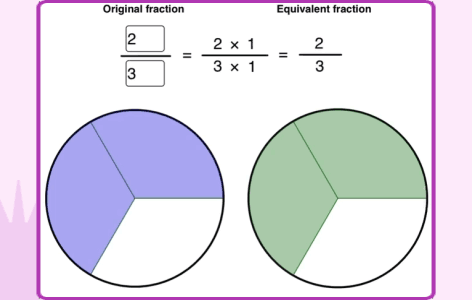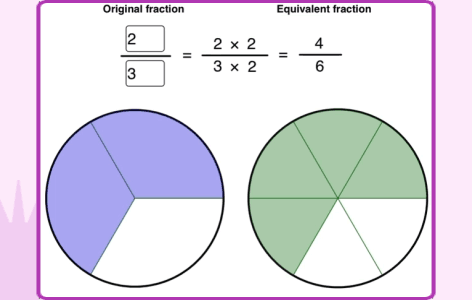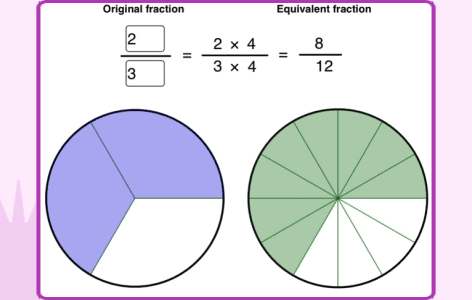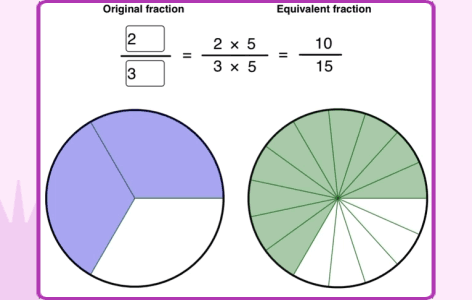
Here students can visualize that when we multiply or divide the numerator and the denominator by the same number the fraction still remains the same.
Measurement and Data
Up to Grade 3, the focus is largely on how to measure length and mass and understand the characteristics of units of measurement. In Grade 4, the common core emphasises on interconversion of units and understanding the metric system as well as the customary system of units. Having developed the conceptual understanding of area and perimeter in Grade 3, in Grade 4, students are expected to solve real world and mathematical problems based on area and perimeter. The common core recommends tasks that help students look at the formula of area as a multiplication equation with an unknown factor.
Here is an example of one such task.
Find the missing values of length, width and area of rectangles given below.

In Cuemath, through examples such as above, students not only convert the area formula to the multiplication equation and find the missing values, but their attention is also drawn to the fact that different rectangles can have the same area.
Geometry
In Grade 4 geometry, Common Core Standards mention identification of 2D shapes that have parallel lines, perpendicular lines and right angles as an important outcome.
In addition to this, for the first time in this grade, the idea of symmetry is introduced. Symmetry is foundational to geometry and it is observed not only in geometrical shapes but in nature too. In Cuemath, students may be encouraged to observe symmetrical patterns in leaves or even in butterflies as shown below.

The line of symmetry divides a shape into two identical halves such that on folding the shape along the line, the two halves completely overlap. In other words, one half is the mirror image of the other.
Symmetry aids in understanding concepts such as reflection, translation or rotation in higher grades. It is imperative to understand that shapes that can just be divided into halves are not necessarily symmetrical. Students should be given opportunities to explore which shapes are symmetrical and which are not.
Let us understand this through this question from the Cuemath curriculum.

Many students would think that the dotted line is a line of symmetry just because it divides the rectangle into two parts that are equal halves. However, this is a misconception that most of us are aware of. How do we address this?
Students may be encouraged to take a paper cutting of this rectangle and fold it along the dotted line as shown below.

The purpose of geometry in primary grades is to develop geometric thinking through visualization. Such an activity will help students visualize that even if the dotted line divides the rectangle into two halves, the two halves do not overlap and hence the dotted line is not a line of symmetry. This will deepen the understanding of the concept and minimize gaps in learning.
A good foundation in mathematics in early years goes a long way in developing mathematical thinking in later years. Hence, in Grade 4, the Cuemath curriculum provides learning experiences of important concepts through concrete and pictorial representations and connects mathematics with the lives of students. Cuemath conducts Live Online Math classes. This makes them love math and see its relevance in their day to day lives. Thus, through a lot of exploratory activities and problem solving, students gradually master numbers and operations, measurement and geometry and become confident and motivated to further delve deep into these concepts in Grade 5.
-By Joyita Banerjee
Joyita heads the curriculum for K-6 and assessments at Cuemath. She has a Master's degree in education and a Post-graduate diploma in Information Technology. With over 15 years of experience, she has expertise in designing and developing curriculum for students and training teachers in math education and educational assessments. Her passion lies in helping children from different social classes master math concepts. In her free time, she loves reading, listening to music and spending time with her family.