A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Find the speed of the train

Solution:

Let the speed of the train be s km/hr and the time taken be t hours.

Distance = Speed × Time

360 = s × t

⇒ t = 360 / s

Increased speed of the train can be written as s + 5

New time to cover the same distance = t - 1

(s + 5) × (t - 1) = 360 ....(1)

st - s + 5t - 5 = 360

360 - s + 5(360/s) - 5 = 360 [Since, st = 360 and t = 360 / s]

- s + 1800/s - 5 = 0

- s² + 1800 - 5s = 0

s² + 5s - 1800 = 0

We will solve this quadratic equation by quadratic formula

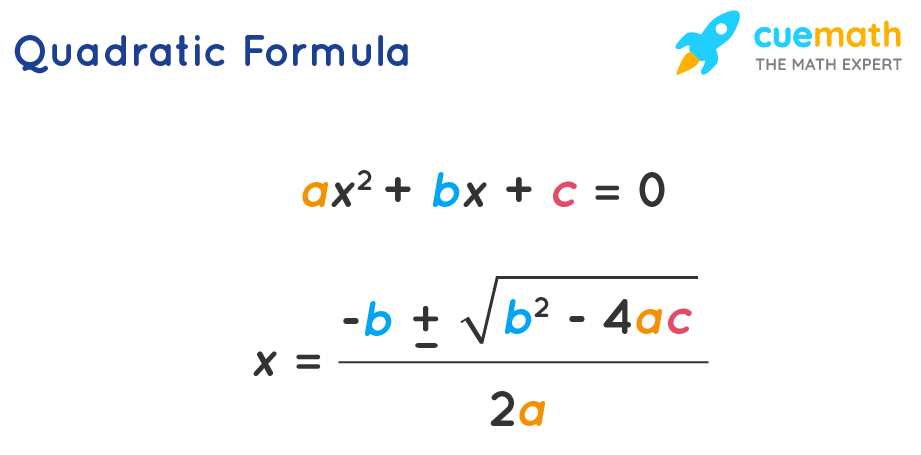
Comparing s² + 5s - 1800 = 0 with ax² + bx + c = 0, we get a = 1, b = 5, c = - 1800

b² - 4ac = (5)² - 4(1)(- 1800)

= 25 + 7200

= 7225 > 0

Hence, the real roots exist.

x = [-b ± √ (b² - 4ac)] / 2a

s = (- 5 ± √ 7225) / 2

s = (- 5 ± 85) / 2

s = (- 5 + 85) / 2 and s = (- 5 - 85) / 2

s = 80 / 2 and s = - 90 / 2

s = 40 and s = - 45

Speed of the train cannot be a negative value.

Therefore, speed of the train is 40 km /hr.

☛ Check: NCERT Solutions for Class 10 Maths Chapter 4

---

Video Solution:

A train travels 360 km at a uniform speed. If the speed had been 5 km /hr more, it would have taken 1 hour less for the same journey. Find the speed of the train

Class 10 Maths NCERT Solutions  Chapter 4 Exercise 4.3 Question 8

Summary:

A train travels 360 km at a uniform speed. If the speed had been 5 km /hr more, it would have taken 1 hour less for the same journey, then the speed of the train is 40 km/hr.

---

☛ Related Questions:

• Find the roots of the following quadratic equations, if they exist, by the method of completing the square. (i) 2x2 - 7 x + 3 = 0(ii) 2x2 + x - 4 = 0(iii) 4x2 + 4√3x + 3 = 0 (iv) 2x2 + x + 4 = 0
• Find the roots of the quadratic equations given in Q.1 above by applying the quadratic formula.
• Find the roots of the following equations:(i) x - 1/x = 3, x ≠ 0(ii) 1/(x + 4) - 1/(x - 7) = 11/30, x ≠ - 4, 7
• The sum of the reciprocals of Rehman’s age (in years) 3 years ago and 5 years from now is 1/3. Find his present age.