Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).

Solution:

Let's draw the given trapezium ABCD

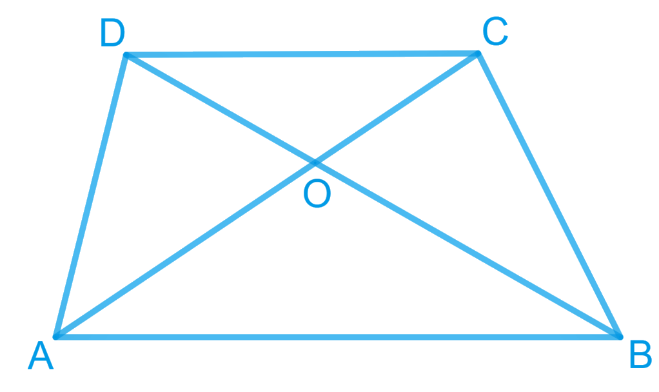
Now, it can be observed that ΔDAC and ΔDBC lie on the same base DC and between the same parallels AB and CD.

According to Theorem 9.2: Two triangles on the same base (or equal bases) and between the same parallels are equal in area.

Area (ΔDAC) = Area (ΔDBC)

Now, Subtracting Area (ΔDOC) from both sides

Area (ΔDAC) - Area (ΔDOC) = Area (ΔDBC) - Area (ΔDOC)

Area (ΔAOD) = Area (ΔBOC) proved.

☛ Check: NCERT Solutions for Class 9 Maths Chapter 9

Video Solution:

Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).

Maths NCERT Solutions Class 9 Chapter 9 Exercise 9.3 Question 10

Summary:

If diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O, then ar (AOD) = ar (BOC).

☛ Related Questions:

• In Fig. 9.27, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that i) ar (ACB) = ar (ACF) ii) ar (AEDF) = ar (ABCDE)
• A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
• ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).[Hint: Join CX.]
• In Fig.9.28, AP || BQ || CR. Prove that ar (AQC) = ar (PBR)