In Fig.9.28, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

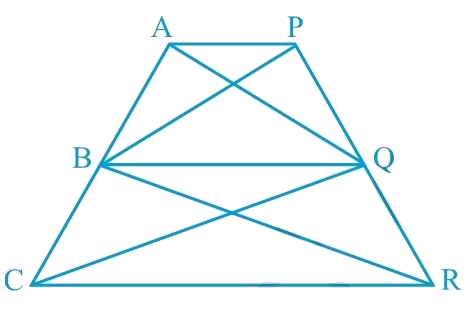
Solution:

Since ∆ABQ and ∆PBQ lie on the same base BQ and are between the same parallels AP and BQ,

According to Theorem 9.2: Two triangles on the same base (or equal bases) and between the same parallels are equal in area.

Area (ΔABQ) = Area (ΔPBQ) ...(1)

Similarly, ∆BCQ and ∆BRQ lie on the same base BQ and are between the same parallels BQ and CR.

Area (ΔBCQ) = Area (ΔBRQ) ... (2)

On adding Equations (1) and (2), we obtain

Area (ΔABQ) + Area (ΔBCQ) = Area (ΔPBQ) + Area (ΔBRQ)

Hence, Area (ΔAQC) = Area (ΔPBR) is proved.

☛ Check: NCERT Solutions Class 9 Maths Chapter 9

Video Solution:

In Fig.9.28, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

Maths NCERT Solutions Class 9 Chapter 9 Exercise 9.3 Question 14

Summary:

In the given figure, if AP || BQ || CR, we have proved that ar (AQC) = ar (PBR).

☛ Related Questions:

• In Fig.9.23, E is any point on median AD of a ∆ ABC. Show that ar (ABE) = ar (ACE).
• In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 1/4 ar(ABC).
• Show that the diagonals of a parallelogram divide it into four triangles of equal area.
• In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar(ABC) = ar (ABD).