Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube
(i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704

Solution:

A number is a perfect cube only when each factor in the prime factorization is grouped in triples. Using this concept, the smallest number can be identified.

(i) 81

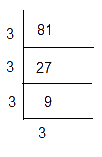
81 = 3 × 3 × 3 × 3

= 3³ × 3

Here, the prime factor 3 is not grouped as a triplet. Hence, we divide 81 by 3, so that the obtained number becomes a perfect cube.

Thus, 81 ÷ 3 = 27 = 3³ is a perfect cube.

Hence the smallest number by which 81 should be divided to make a perfect cube is 3.

(ii) 128

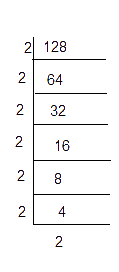
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2

= 2³ × 2³ × 2

Here, the prime factor 2 is not grouped as a triplet. Hence, we divide 128 by 2, so that the obtained number becomes a perfect cube.

Thus, 128 ÷ 2 = 64 = 4³ is a perfect cube.

Hence the smallest number by which 128 should be divided to make a perfect cube is 2.

(iii) 135

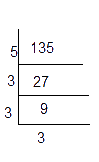
135 = 3 × 3 × 3 × 5

= 3³ × 5

Here, the prime factor 5 is not a triplet. Hence, we divide 135 by 5, so that the obtained number becomes a perfect cube.

135 ÷ 5 = 27 = 3³ is a perfect cube.

Hence the smallest number by which 135 should be divided to make a perfect cube is 5.

(iv) 192

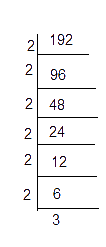
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3

= 2³ × 2³ × 3

Here, the prime factor 3 is not grouped as a triplet. Hence, we divide 192 by 3, so that the obtained number becomes a perfect cube.

192 ÷ 3 = 64 = 4³ is a perfect cube

Hence the smallest number by which 192 should be divided to make a perfect cube is 3.

(v) 704

704 = 2 × 2 × 2 × 2 × 2 × 2 × 11

= 2³ × 2³ × 11

Here, the prime factor 11 is not grouped as a triplet. Hence, we divide 704 by 11, so that the obtained number becomes a perfect cube.

Thus, 704 ÷ 11 = 64 = 4³ is a perfect cube

Hence the smallest number by which 704 should be divided to make a perfect cube is 11.

☛ Check: NCERT Solutions for Class 8 Maths Chapter 7

---

Video Solution:

Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube (i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704

NCERT Solutions for Class 8 Maths Chapter 7 Exercise 7.1 Question 3

Summary:

The smallest number by which each of the following numbers must be divided to obtain a perfect cube (i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704 are (i) 3, (ii) 2, (iii) 5, (iv) 3, and (v) 11

---

☛ Related Questions:

• Which of the following numbers are not perfect cubes?(i) 216 (ii) 128 (iii) 1000 (iv) 100 (v) 46656
• Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.(i) 243 (ii) 256 (iii) 72 (iv) 675 (v) 100
• Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
• Find the cube root of each of the following numbers by prime factorization method. (i) 64 (ii) 512 (iii) 10648 (iv) 27000 (v) 15625 (vi) 13824 (vii) 110592 (viii) 46656 (ix) 175616 (x) 91125