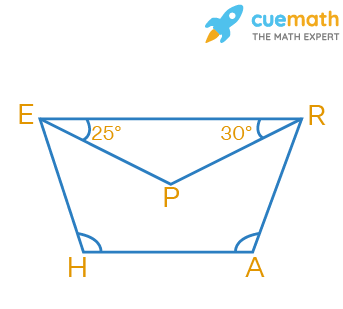
In trapezium HARE, EP and RP are bisectors of ∠E and ∠R respectively. Find ∠HAR and ∠EHA.
Solution:
Given, HARE is a trapezium.
EP and RP are bisectors of ∠E and ∠R.
We have to find ∠HAR and ∠EHA.
We know that adjacent angles of a trapezium are supplementary.
So, ∠E + ∠H = 180°
Since EP is the angle bisector of ∠E,
∠PER + ∠PEH + ∠EHA = 180°
25° + 25° + ∠EHA = 180°
50° + ∠EHA = 180°
∠EHA = 180° - 50°
∠EHA = 130°
Similarly, ∠R + ∠A = 180°
Since RP is the angle bisector of ∠R,
∠ERP + ∠PRA + ∠HAR = 180°
30° + 30° + ∠HAR = 180°
60° + ∠HAR = 180°
∠HAR = 180° - 60°
∠HAR = 120°
Therefore, the required angles are 130° and 120°.
✦ Try This: Find the values of x, y, z and w in the given figure.
☛ Also Check: NCERT Solutions for Class 8 Maths
NCERT Exemplar Class 8 Maths Chapter 5 Problem 154
In trapezium HARE, EP and RP are bisectors of ∠E and ∠R respectively. Find ∠HAR and ∠EHA.
Summary:
In trapezium HARE, EP and RP are bisectors of ∠E and ∠R respectively. The values of ∠HAR and ∠EHA are 120° and 130°.
☛ Related Questions: