Angle Bisector
An angle bisector is defined as a ray, segment, or line that divides a given angle into two angles of equal measures. The word bisector or bisection means dividing one thing into two equal parts. In geometry, we usually divide a triangle and an angle by a line or ray which is considered as an angle bisector.
| 1. | What is Angle Bisector? |
| 2. | Angle Bisector of a Triangle |
| 3. | Properties of an Angle Bisector |
| 4. | Angle Bisector Construction |
| 5. | Angle Bisector Theorem |
| 6. | FAQs on Angle Bisector |
What is Angle Bisector?
The angle bisector in geometry is the ray, line, or segment which divides a given angle into two equal parts. For example, an angle bisector of a 60-degree angle will divide it into two angles of 30 degrees each. In other words, it divides an angle into two smaller congruent angles. Given below is an image of an angle bisector of ∠AOB.
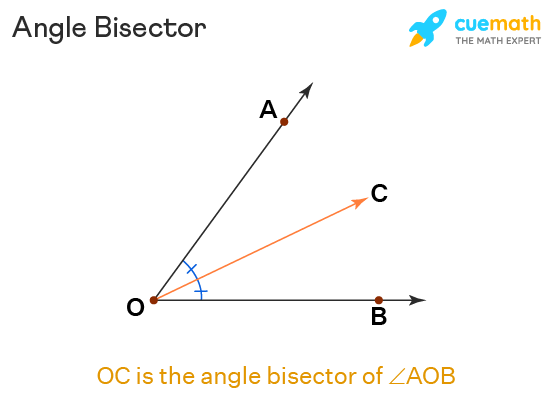
Angle Bisector of a Triangle
In a triangle, the angle bisector of an angle is a straight line that divides the angle into two equal or congruent angles. There can be three angle bisectors in every triangle, one for each vertex. The point where these three angle bisectors meet in a triangle is known as its incenter. The distance between the incenter to all the vertices of a triangle is the same. Look at the image below showing the angle bisector of a triangle. Here, AG, CE, and BD are the angle bisectors of ∠BAC, ∠ACB, and ∠ABC respectively. F is the point of intersection of all three bisectors which is known as incenter and it is at an equal distance from each of the vertex.
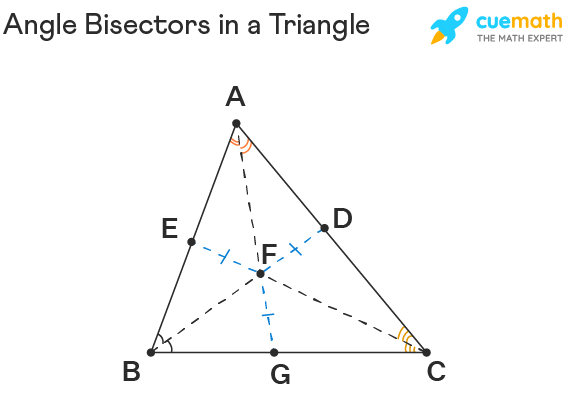
Properties of an Angle Bisector
Till now you must be clear about the meaning of angle bisector in geometry. Now, let us learn some of the angle bisector properties listed below:
- An angle bisector divides an angle into two equal parts.
- Any point on the bisector of an angle is equidistant from the sides or arms of the angle.
- In a triangle, it divides the opposite side into the ratio of the measure of the other two sides.
Construction of Angle Bisector
Let's try constructing the angle bisector for an angle. In this section, we will see the steps to be followed for angle bisector construction.
Steps to Construct an Angle Bisector:
Step 1: Draw any angle, say ∠ABC.
Step 2: Taking B as the center and any appropriate radius, draw an arc to intersect the rays BA and BC at, say, E and D respectively. (Refer to the figure below)

Step 3: Now, taking D and E as centers and with the same radius as taken in the previous step, draw two arcs to intersect each other at F.
Step 4: Join B to F and extend it as a ray. This ray BF is the required angle bisector of angle ABC.

Angle Bisector Theorem
Let's now understand in detail an important property of the angle bisector of a triangle as stated in the previous section. This property is known as the angle bisector theorem of a triangle. According to the angle bisector theorem, in a triangle, the angle bisector drawn from one vertex divides the side on which it falls in the same ratio as the ratio of the other two sides of the triangle.
Statement: An angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides of the triangle.

In the above image, PS is the angle bisector of ∠P in ΔPQR. Therefore, by applying the angle bisector theorem we can say that PQ/PR = QS/SR or a/b = x/y.
► Related Articles
Check these interesting articles related to the angle bisector in math.
Angle Bisector Examples
-
Example 1: In the figure given below, BD is the bisector of ∠ABC and BE bisects ∠ABD. Find the measure of ∠DBE given that ∠ABC=80°.

Solution:
It is given that ∠ABC=80°.
Also, ∠ABD = 1/2 × ∠ABC = 1/2 × 80° = 40° (BD is an angle bisector bisecting ∠ABC into two equal parts)
Now, ∠DBE = 1/2 × ∠ABD = 1/2 × 40° = 20° (BE is a bisector and bisects ∠ABD into two equal parts)
∴ The value of ∠DBE is 20°. -
Example 2: In the figure, the ray drawn from point O is the angle bisector of ∠BON. Find x.

Solution:
To find x, we will be using the property: Any point on the bisector of an angle is equidistant from the sides of the angle.
So, the bisector drawn from O will be equidistant from sides OB and ON.
⇒ 3x − 2 = 10
⇒ 3x = 2 + 10
⇒ 3x = 12
∴ The value of x is 4. -
Example 3: If QS is the bisector of ∠PQR, find x.

Solution:
As QS bisects ∠PQR, by angle bisector theorem we get, QP/QR = PS/RS.
⇒ 18/24 = 12/x
⇒ x = (12 × 24)/18
⇒ x = (2 × 24)/3 = 2 × 8 = 16
∴ The value of x is 16.

FAQs on Angle Bisector
What is an Angle Bisector?
An angle bisector is the ray, line, or line segment which divides an angle into two congruent angles.
What are the Properties of Angle Bisector?
An angle bisector has two main properties:
- Any point on the bisector of an angle is equidistant from the sides of the angle.
- In a triangle, the angle bisector divides the opposite side in the ratio of the adjacent sides.
What is an Angle Bisector of a Triangle?
The angle bisector of a triangle drawn from any of the three vertices divides the opposite side in the ratio of the other two sides of the triangle. There can be three angle bisectors drawn in a triangle.
Does Angle Bisector Cut an Angle in Half?
Yes, an angle bisector divides the given angle into two equal angles. In other words, we can say that the measure of each of these angles is half of the original angle.
How to Construct an Angle Bisector?
An angle bisector construction can be done by following the steps given below:
- Step 1: Take a compass and take any suitable width on it. Place its tip on the vertex of the angle and draw an arc touching the arms of the angle at two distinct points.
- Step 2: Keep the same width of the compass and draw arcs intersecting each other from each of those two points.
- Step 3: Draw a ray from the vertex of the angle to the point of intersection formed in the previous step.
- Step 4: That ray will be the required angle bisector of the given angle.
What is the Property of Angle Bisector of Triangle?
The property of the angle bisector of a triangle states that the angle bisector divides the opposite side of a triangle in the ratio of its adjacent sides.
Does the Angle Bisector go through the Midpoint?
It is not always true that an angle bisector goes through the midpoint of the opposite side. It divides the opposite side in proportion to the adjacent sides of the triangle.
Can an Angle have More Than One Angle Bisector?
No, an angle can have only one angle bisector. For example, if we bisect a 60° angle we will get two 30° angles as a result. This means 60° angle is divided into two equal angles (30° each). Hence, 60° angle can only be bisected once. Further, we can again bisect 30° angle into two equal angles as 15° each.
visual curriculum