Congruent Angles
Congruent angles are the angles that have equal measure. So all the angles that have equal measure will be called congruent angles. They are seen everywhere, for example, in equilateral triangles, isosceles triangles, or when a transversal intersects two parallel lines. Let us learn more about the congruence of angles along with their construction in this article.
| 1. | What are Congruent Angles? |
| 2. | Congruent Angles Theorem |
| 3. | Constructing Congruent Angles |
| 4. | FAQs on Congruent Angles |
What are Congruent Angles?
In mathematics, the definition of congruent angles is "angles that are equal in the measure are known as congruent angles". In other words, equal angles are congruent angles. It is denoted by the symbol "≅", so if we want to represent ∠A is congruent to ∠X, we will write it as ∠A ≅ ∠X. Look at a congruent angles example given below.

In the above image, both the angles are equal in measurement (60∘ each). They can completely overlap each other. So, as per the definition, we can say that both the given angles are congruent angles.
Congruent Angles Theorem
There are many theorems based on congruent angles. Using the congruent angles theorem we can easily find out whether two angles are congruent or not. Those theorems are listed below:
- Vertical angles theorem
- Corresponding angles theorem
- Alternate angles theorem
- Congruent supplements theorem
- Congruent complements theorem
Let's understand each of the theorems in detail along with its proof.
Vertical Angles Theorem
According to the vertical angles theorem, vertical angles are always congruent. Let us check the proof of it.
Statement: Vertical angles are congruent.
Proof: The proof is simple and is based on straight angles. We already know that angles on a straight line add up to 180°.

So in the above figure:
| Statement | Reason |
|---|---|
| ∠1+∠2 = 180° | Linear Pair |
| ∠1+∠4 = 180° | Linear Pair |
| ∴ ∠1+∠2 = 180∘ = ∠1+∠4 | By equating the above two equations |
| ∴ ∠1+∠2 =∠1+∠4 | Quantities equal to the same quantity are equal to each other. (Transitive: if a=b and b=c that implies a=c) |
| ∴ ∠2 =∠4 | If equals are subtracted from equals, the differences are equal. (By eliminating ∠1 on both sides) |
| Also, ∠1=∠3 | Similarly, we can prove for ∠1 and ∠3 |
Conclusion: Vertically opposite angles are always congruent angles.
Corresponding Angles Theorem
The corresponding angles definition tells us that when two parallel lines are intersected by a third one, the angles that occupy the same relative position at each intersection are known to be corresponding angles to each other.
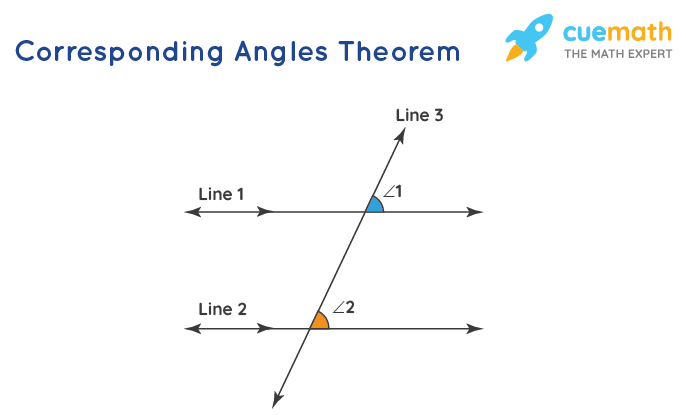
When a transversal intersects two parallel lines, corresponding angles are always congruent to each other. In this figure, ∠1 = ∠2. It's a postulate so we do not need to prove this. It is always stated as true without proof.
Alternate Angles Theorem
When a transversal intersects two parallel lines, each pair of alternate angles are congruent.

Refer to the figure above. We have:
∠1 = ∠5 (corresponding angles)
∠3 = ∠5 (vertically opposite angles)
Thus, ∠1 = ∠3
Similarly, we can prove the other three pairs of alternate congruent angles too.
Congruent Supplements Theorem
Supplementary angles are those whose sum is 180°. This theorem states that angles supplement to the same angle are congruent angles, whether they are adjacent angles or not.

We can prove this theorem by using the linear pair property of angles, as,
∠1+∠2 = 180° (Linear pair of angles)
∠2+∠3 = 180° (Linear pair of angles)
From the above two equations, we get ∠1 = ∠3.
∴ Angles supplement to the same angle are congruent angles.
Congruent Complements Theorem
Complementary angles are those whose sum is 90°. This theorem states that angles that complement the same angle are congruent angles, whether they are adjacent angles or not. Let us understand it with the help of the image given below.
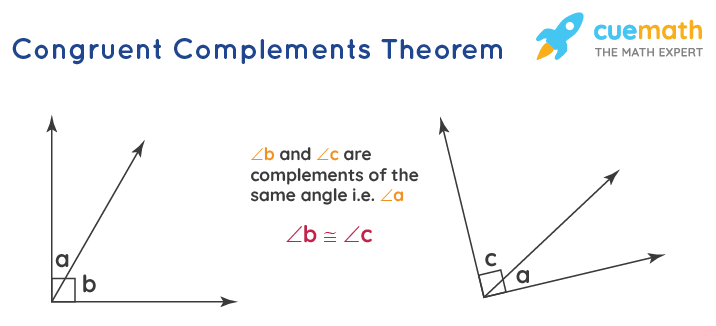
We can easily prove this theorem as both the angles formed are right angles.
∠a+∠b = 90° (∵∠a and ∠b form 90° angle)
∠a+∠c = 90° (∵∠a and ∠c form 90° angle)
So, from the above two equations, we get, ∠b ≅ ∠c.
∴ Two angles complementary to the same angle are congruent angles.
Constructing Congruent Angles
In this section, we will learn how to construct two congruent angles in geometry. There are two cases that come up while learning about the construction of congruent angles, and they are:
- Construction of two congruent angles with any measurement.
- Construction of a congruent angle to the given angle.
Construction of Two Congruent Angles
Let's learn the construction of two congruent angles step-wise.
Step 1- Draw two horizontal lines of any suitable length with the help of a pencil and a ruler or a straightedge.

Step 2- Take any arc on your compass, less than the length of the lines drawn in the first step, and keep the compass tip at the endpoint of the line. Draw the arc keeping the lines AB and PQ as the base without changing the width of the compass.

Step 3 - Keep the compass tip on point D and expand the legs of the compass to draw an arc of any suitable length. Draw that arc and repeat the same process with the same arc by keeping the compass tip on point S.

Step 4- Draw lines that will join AC and PR.

This is how we get two congruent angles in geometry, ∠CAB, and ∠RPQ.
Construction of a Congruent Angle to the Given Angle
By now, you have learned about how to construct two congruent angles in geometry with any measurement. But what if any one angle is given and we have to construct an angle congruent to that? Let's learn it step-wise.
Suppose an angle ∠ABC is given to us and we have to create a congruent angle to ∠ABC.

Step 1 - Draw a horizontal line of any suitable measurement and name it YZ.

Step 2 - Keep compass tip at point B in the given angle and draw an arc by keeping BC as the base and name that point D.

Step 3 - With the same width, draw an arc by keeping the compass tip at point Y and name the point at line YZ as O.

Step 4 - Keep compass tip at point D and measure the arc from point D to the point of intersection of the arc at segment AB.
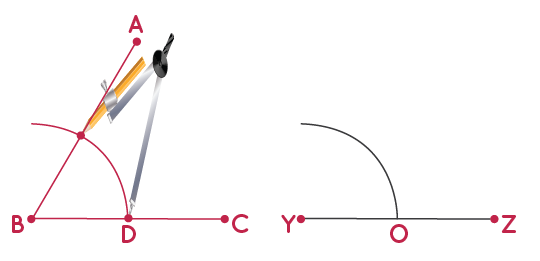
Step 5 - With the same arc, keep your compass tip at point O and mark a cut at the arc drawn in step 3, and name that point as X.

Step 6 - Draw a line and join points X and Y.

Here, we get ∠ABC ≅ ∠XYZ, which satisfies the definition of the congruent angle. This is how we can construct an angle congruent to the given angle.
Congruent Angles Tips and Tricks:
- Congruent angles are just another name for equal angles.
- All vertically opposite angles are congruent angles.
- All alternate angles and corresponding angles formed by the intersection of two parallel lines and a transversal are congruent angles.
- According to the definition of congruent angles "For any two angles to be congruent, they need to be of the same measurement."
► Related Topics
Check these interesting articles related to congruent angles definition.
Congruent Angles Examples
-
Example 1: Find the measurement of angle f.

Solution:
Here, ∠DOE and ∠AOC are congruent (vertical) angles. So, ∠DOE = ∠AOC.
113∘ = 90º+f
f = 113°-90°
f = 23°
Therefore, the value of f is 23 degrees.
-
Example 2: Did you ever have a parallelogram-shaped lunchbox in school? How did you close this tiffin box? You tried to find the best match of angles on the lid to close the box. Is that right? Can you think of any reason why you did that?
Solution:
The reason you did this was that you tried to find the best fit of congruent angles for closing the lid of the box. As we know that corresponding angles are congruent, you tried to find the angles on the lid that best matched every corner’s corresponding angles in the box.
You were observing the geometry of the corresponding angles without realizing it.

Answer: The angles in a tiffin box are congruent angles.
-
Example 3: If the given figure, two lines are parallel and are intersected by a transversal. What will be the measure of ∠x and ∠y?

Solution:
The given lines are parallel and according to the congruent alternate angles theorem, the given angle of measure 85∘ and ∠x are alternate congruent angles. So, 85∘ = ∠x.
Similarly, 95∘ and y are congruent alternate angles. So, 95∘ = ∠y.Therefore, the value of ∠x is 85°, and ∠y is 95°.

FAQs on Congruent Angles
What does Congruent Angles mean?
Two angles are said to be congruent when they are of equal measurement and can be placed on each other without any gaps or overlaps. The congruent angles symbol is ≅.
What are the Conditions Required for Congruent Angles?
There is only one condition required for angles to be congruent and that is, they need to be of the same measurement.
Do Congruent Angles Add up to 180?
In general, all congruent angles are not supplementary angles. For angles to add up to 180, they must be supplementary angles. So only right angles are congruent as well as supplementary angles because they have the same measure and they add up to 180.
Are Right Angles Congruent?
Right angles are always congruent as their measurement is the same. They always measure 90°.
What are Congruent Angles in Parallel Lines?
When two parallel lines are intersected by a transversal, we get some congruent angles which are corresponding angles, vertical angles, alternate interior angles, and alternate exterior angles.
How do we Know if Angles are Congruent?
Two angles are congruent if their measurement is the same. So, we can check the angle measurement of the given angles with the help of a protractor to know whether the given angles are congruent or not.
Are Congruent Angles Equal?
Yes, congruent angles are equal angles.
How to Find Congruent Angles?
Any two angles of the same measurement are congruent angles. So, to find congruent angles, we just have to identify all equal angles. When placed on top of each other, they completely fit without any gaps.
What Type of Angles are always Congruent?
Vertically opposite angles, alternate angles, and corresponding angles, drawn on parallel lines and transversals are always congruent. In addition to that, angles supplementary to the same angle and angles complementary to the same angle are also congruent angles.
visual curriculum