Geometric construction
In this mini-lesson, we will explore the world of geometric constructions in math. You will get to learn about the way to construct perpendicular bisector, angle bisector, parallel lines and other interesting facts around the topic. You can try your hand at solving a few interesting practice questions at the end of the page.
Austin is a civil engineer.
He needs an accurate map to construct a building and design the tools.

To draw such figures, he uses some basic geometrical instruments like a graduated scale, a pair of set-squares, divider, compass, and ruler.
We don't want you to worry, and get your geometric instruments ready as we, at Cuemath, are here to help you understand the geometric constructions in a clear way.
In this short lesson, we will learn some basic geometric constructions.
Lesson Plan
What Is Geometric Construction?
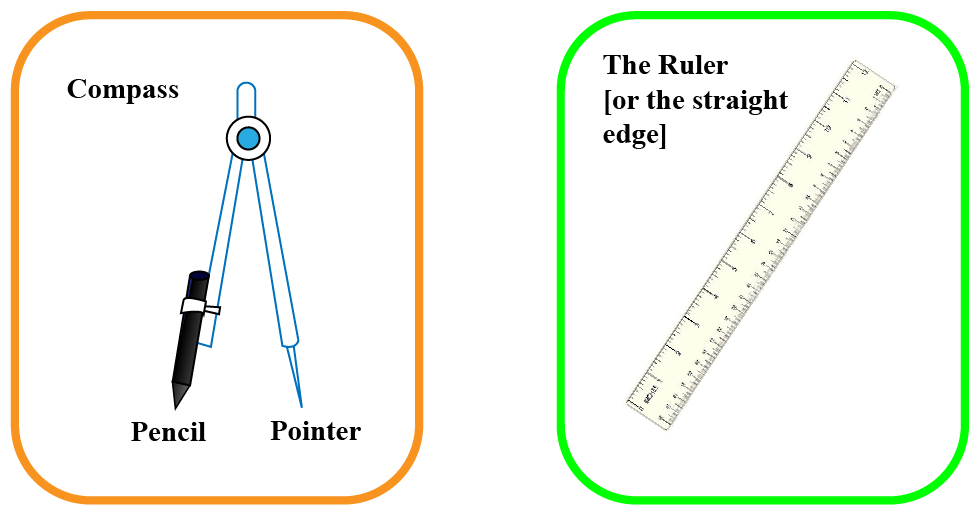
Geometric construction is the process of drawing a geometrical figure using two geometrical instruments, a compass, and a ruler.
We use a compass to draw arcs and circles and mark off equal lengths.
We use a ruler to draw line segments and measure their lengths.
How To Construct Perpendicular Bisector?
To carry out this construction, we will use the fact that any point on the perpendicular bisector of a line segment is equidistant from the two end-points of the line segment.
Suppose we have a line segment \(\overline{AB}\).

The steps in the construction are outlined below.
Step 1: Taking A and B as centers, and a radius of more than half of \(\overline{AB}\), draw arcs on both sides of \(\overline{AB}\), to intersect each other, as shown below.

The reason you require the radius of your arcs to be more than half of \(\overline{AB}\) is that if the radius is less than half of \(\overline{AB}\), the arcs will not intersect (try it!).
Step 2: Let the two points of the intersection so obtained be P and Q. Draw a line through P and Q. This is the required perpendicular bisector.

Here, POQ is the perpendicular bisector of \(\overline{AB}\).
You can visualize these steps in the simulation below by clicking the 'GO' button.
Steps For Constructing Parallel Lines
Isn't it interesting to realize the fact that these orange and green lines will go on forever but will never meet?

These two lines are parallel to each other.
We will learn how to construct parallel lines using a ruler and a compass.
Let \(\overleftrightarrow{AB}\) be a line and P be a point outside the line \(\overleftrightarrow{AB}\).

Step 1: Draw a transversal through the point P intersecting the line \(\overleftrightarrow{AB}\), say at X.

Step 2: Taking X as a center and any radius, draw an arc intersecting the segment \(\overline{PX}\) at M and \(\overleftrightarrow{AB}\) at point N.

Step 3: Now, taking P as a center and the same radius, draw an arc EF intersecting the segment \(\overline{PX}\) at Q.

Step 4: Taking Q as a center and same radius, draw an arc intersecting the arc EF at R.

Step 5: Join R and P and extend it on both sides to draw the line \(\overleftrightarrow{CD}\).

Here, the line \(\overleftrightarrow{CD}\) is parallel to the line \(\overleftrightarrow{AB}\).
Experiment with the simulation below to visualize this process by clicking the 'GO' button.
How To Construct an Angle Bisector?
Suppose we have \(\angle PQR\) and we want to bisect this angle.

Follow the steps of construction mentioned below:
- Let Q be the center and with any radius, draw an arc intersecting the ray \(\overrightarrow{QP}\) and \(\overrightarrow{QR}\), say at the points E and D respectively.
- Now, taking D and E as centers and the same radius, draw arcs intersecting each other say at F.
- Draw the ray \(\overrightarrow{QF}\).

Here, \(\overrightarrow{QP}\) is the angle bisector of \(\angle PQR\).
Use the simulation below to visualize the steps of construction for angle bisector by clicking the 'GO' button.
Solved Examples
| Example 1 |
The green and blue lines are parallel, and M and N are points on the green and blue lines respectively.
If the shortest distance from M to the blue line is 6 units.

What will be the shortest distance from N to the green line?
Solution
The given lines are parallel, so they are equidistant throughout.
This means that the perpendicular distance from M to the blue line is equal to the perpendicular distance from N to the green line. Hence, this distance is equal to 6 units.
In fact, the shortest distance between the two lines is the perpendicular distance between them.
| So, the shortest distance from N to the green line is 6 units. |
| Example 2 |
Ryan is flying a kite.

The kite has two angles bisected as shown below.

Can you find the measures of the angles \(\angle EKI\) and \(\angle ITE\)?
Solution
The angles \(\angle EKI\) and \(\angle ITE\) are bisected by the line \(\overleftrightarrow{KT}\).
\(\overleftrightarrow{KT}\) divides the angles \(\angle EKI\) and \(\angle ITE\) in two equal angles respectively.
Thus,
\(\angle EKI=2\times 45^{\circ}=90^{\circ}\) and
\(\angle ITE=2\times 27^{\circ}=54^{\circ}\)
| \(\therefore\) \(\angle EKI=90^{\circ}\) and \(\angle ITE=54^{\circ}\). |
| Example 3 |
Ms. Amy asked Mia to justify the construction of a perpendicular bisector of a line segment.

Can you help her justify this?
Solution
In \(\Delta PAQ\) and \(\Delta PBQ\):
1. PA = PB (arcs of equal radius)
2. QA = QB (again, arcs of equal radius)
3. PQ = PQ (common)
By the SSS criterion, the two triangles are congruent, which means that \(\angle APO\) = \(\angle BPO\).
In \(\Delta APO\) with \(\Delta BPO\):
1. PA = PB (arcs of equal radius)
2. \(\angle APO\) = \(\angle BPO\) (just shown)
3. PO = PO (common)
By the SAS criterion, the two triangles are congruent, which means that AO = BO, and also:
\(\angle AOP\) = \(\angle BOP\) = \(\dfrac{1}{2}180^0 = 90^0\)
| \(\therefore\), POQ is the perpendicular bisector of AB. |
| Example 4 |
\(\angle PQR\) is divided into different angles.

Can you determine the angle bisector of \(\angle PQR\)?
Solution
Notice that,
\[\begin{align}\angle PQT&=\angle PQV + \angle VQT \\&= 50^{\circ}+ 10^{\circ}\\&= 60^{\circ}\end{align}\]
\[\begin{align}\angle TQR&= \angle TQS + \angle SQR \\ &= 35^{\circ}+ 25^{\circ}\\&= 60^{\circ}\end{align}\]
This means that \(\angle PQT=\angle TQR\).
| So, ray QT is the angle bisector of \(\angle PQR\). |
Be careful while doing geometric constructions.
Here are a few tips and tricks for you to follow while doing construction.

- Always draw thin lines and mark the points lightly.
- Keep your instruments like a compass, ruler, and divider with sharp tips and sharp edges.
- Always keep 2 pencils in your geometry box, one for insertion in the compass and the other to draw lines and mark points.
Interactive Questions
Here are a few activities for you to practice.
Select/type your answer and click the "Check Answer" button to see the result.
Let's Summarize
The mini-lesson targeted the fascinating concept of geometric constructions. The math journey around geometric constructions starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever. Here lies the magic with Cuemath.
About Cuemath
At Cuemath, our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.
Frequently Asked Questions (FAQs)
1. What are the parallel lines?
Parallel lines are a pair of lines that never cut (intersect) or meet each other, and they lie on the same plane.

2. What is the purpose of geometric constructions?
Geometric constructions help us to draw lines, angles, and shapes with simple tools.
