A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.

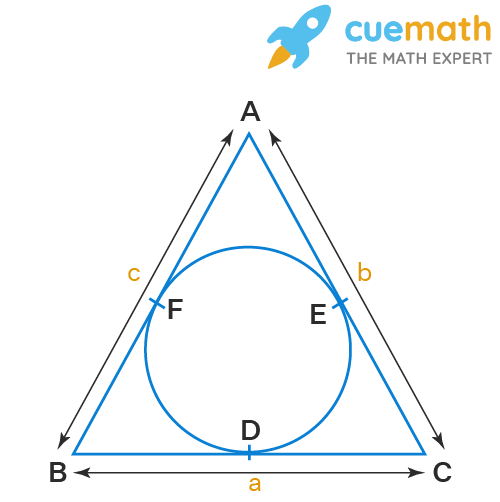
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s - b

Solution:

Given, s denotes the semiperimeter of a triangle ABC.

The sides of triangle BC = a, CA = b and AB = c.

A circle touches the sides BC, CA, AB at D, E and F

We have to prove that BD = s - b

Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s - b

Semiperimeter of atriangle is half the sum of the sides of the triangle.

Semiperimeter of a triangle is given by

s = (a + b + c)/2

We know that the tangents to a circle through an external point are equal.

The tangents through point A are AF and AE

So, AF = AE -------------------- (1)

The tangents through point B are BF and BD

So, BF = BD -------------------- (2)

The tangents through point C are CD and CE

So, CD = CD -------------------- (3)

Semiperimeter, s = (AB + BC + CA)/2

2s = AB + BC + CA

From the figure,

AB = AF + FB

BC = BD + DC

CA = CE + EA

2s = AF + FB + BD + DC + CE + EA

From (1), (2) and (3),

2s = AE + AE + CE + CE + BD + BD

2s = 2AE + 2CE + 2BD

2s = 2(AE + CE + BD)

Cancelling out common term,

s = AE + CE + BD

From the figure,

AC = AE + CE

So, s = AC + BD

We know AC = b

s = b + BD

BD = s - b

Therefore, it is proven that BD = s - b

✦ Try This: ABC is a triangle A circle touches sides AB and AC produced and side BC at X, Y and z respectively. Show that AX= 1/2 Perimeter of ΔABC.

☛ Also Check: NCERT Solutions for Class 10 Maths Chapter 10

NCERT Exemplar Class 10 Maths Exercise 9.4 Problem 2

Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s - b

Summary:

Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively. It is proven that BD = s - b

☛ Related Questions:

Math worksheets and
visual curriculum