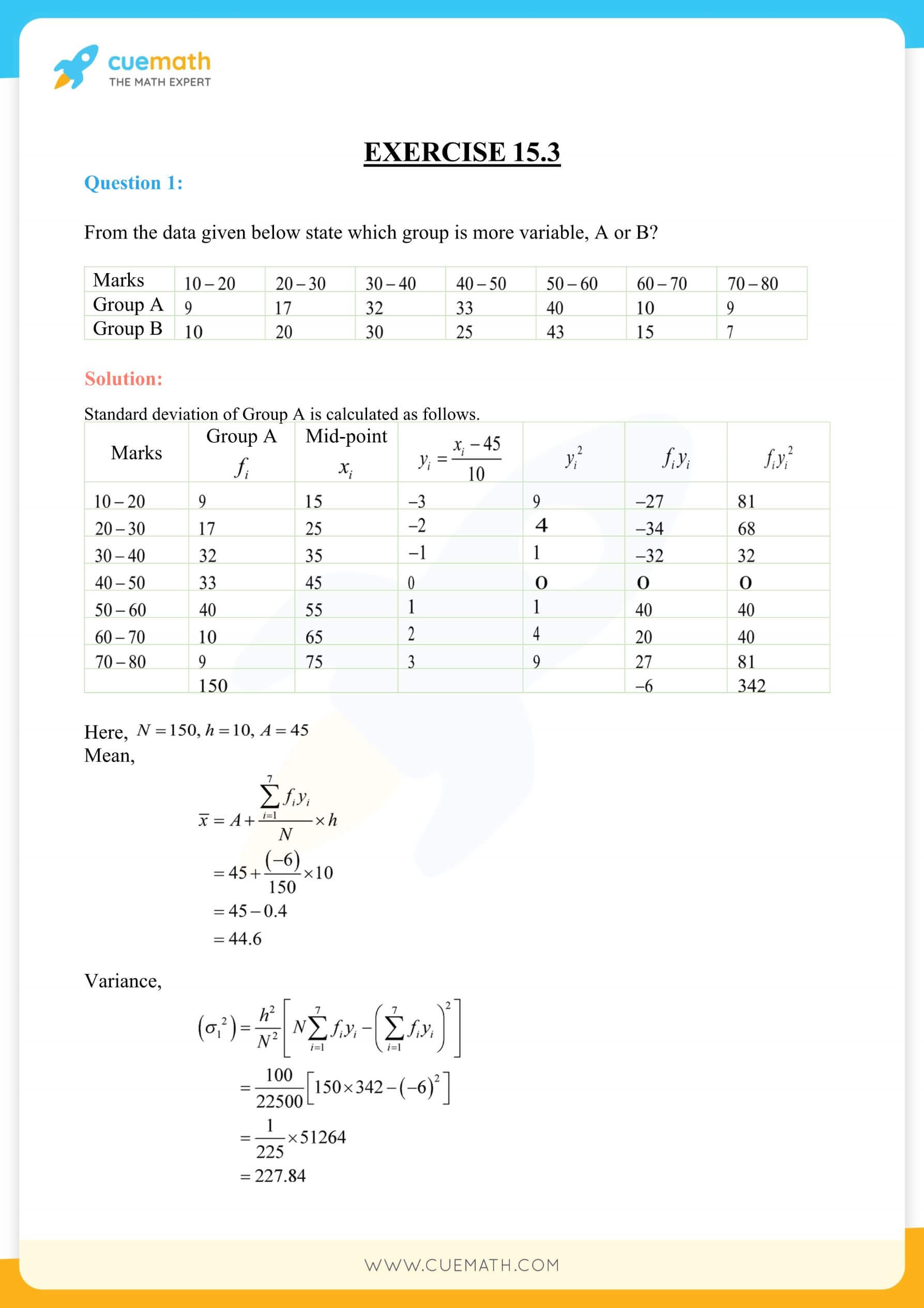
NCERT Solutions Class 11 Maths Chapter 15 Exercise 15.3 Statistics
NCERT solutions for class 11 maths chapter 15 exercise 15.3 statistics focuses on the coefficient of variation. It can be defined as the measure of variability that is independent of units. Whenever we want to compare the variability of two series with the same mean, which are measured in different units, we do not merely calculate the measures of dispersion such as mean deviation or standard deviation but we require such measures which are independent of the units. Another subsection of this topic includes the comparison of two frequency distributions with the same mean. NCERT solutions class 11 maths chapter 15 exercise 15.3 has 5 problems. It is necessary to be confident with the previous exercises as the coefficient of variation is just an extension of those.
The coefficient of variation sees the use of the mean as well as the standard deviation. This quantity does not have any units. All the questions in the exercise are of a medium level however, they are long answer sums. Thus, kids should constantly practice this topic so as to build up a respectable speed while attempting such problems in examinations. The class 11 maths NCERT solutions chapter 15 exercise 15.3 statistics can be accessed by clicking on the link given below:
☛ Download NCERT Solutions Class 11 Maths Chapter 15 Exercise 15.3
Exercise 15.3 Class 11 Chapter 15








More Exercises in Class 11 Maths Chapter 15
- NCERT Solutions Class 11 Maths Chapter 15 Ex 15.1
- NCERT Solutions Class 11 Maths Chapter 15 Ex 15.2
- NCERT Solutions Class 11 Maths Chapter 15 Miscellaneous Ex
NCERT Solutions Class 11 Maths Chapter 15 Exercise 15.3 Formulas
NCERT solutions class 11 maths chapter 15 exercise 15.1 statistics use the formulas of the mean and standard deviation given in previous exercises as well as sees the introduction of the coefficient of variation. This formula is given as:
- V. = σ / x̅ where x̅ ≠ 0, σ is the standard deviation and x̅ is the mean that can be calculated by methods listed earlier in this chapter.
For comparing the variability or dispersion of two series, we calculate the coefficient of variance for each series. The series having greater C.V. is said to be more variable than the other. The series having lesser C.V. is said to be more consistent than the other.
Download Cuemath NCERT Solutions PDF for free and start learning!
visual curriculum