A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.

Verify Euler’s formula for these solids.
Verify Euler’s formula for these solids.

Solution:

According to Euler’s formula, in any polyhedron, F + V - E = 2, where ‘F’ stands for the number of faces, ‘V’ stands for the number of vertices and ‘E’ stands for the number of edges.

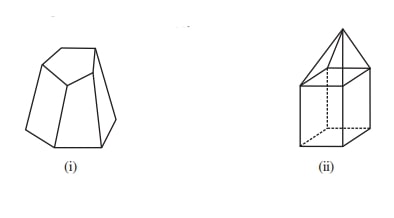
(i) In the figure we can see that top and bottom faces are pentagons.

Number of faces, F = 7

Number of edges, E =15

Number of vertices, V =10

Let’s verify Euler’s formula,

F + V - E = 7 + 10 - 15

= 17 - 15 = 2

Thus, Euler's formula is verified.

(ii) In the figure we can see that its top is a square pyramid and the bottom is a square prism.

Number of faces, F = 9

Number of edges, E = 16

Number of vertices, V = 9

Let’s verify Euler’s formula,

F + V - E = 9 + 9 - 16

= 18 - 16 = 2

Thus, Euler's formula is verified.

☛ Check: NCERT Solutions for Class 8 Maths Chapter 10

Video Solution:

Verify Euler’s formula for these solids

Maths NCERT Solutions Class 8 Chapter 10 Exercise 10.3 Question 6

Summary:

Euler’s formula for the given solids is verified.

☛ Related Questions:

Math worksheets and
visual curriculum