Binary Multiplication
Binary multiplication is the process of multiplying binary numbers. The process of multiplying binary numbers is the same as that of arithmetic multiplication with decimal numbers. The only difference is that binary multiplication involves numbers that are consist of 0s and 1s, whereas, decimal multiplication involves numbers that comprise digits from 0 to 9. Let us learn the process of binary multiplication step by step.
| 1. | Binary Multiplication Rules |
| 2. | How to Multiply Binary Numbers? |
| 3. | Binary Multiplication Examples |
| 4. | Practice Questions on Binary Multiplication |
| 5. | FAQs on Binary Multiplication |
Binary Multiplication Rules
Binary multiplication is similar to the multiplication of decimal numbers. We have a multiplier and a multiplicand. The result of multiplication results in a product. Since only binary digits are involved in binary multiplication, we get to multiply only 0s and 1s. The rules for binary multiplication are as follows.
| Multiplicand | Multiplier | Product |
|---|---|---|
| 0 | 0 | 0 × 0 = 0 |
| 0 | 1 | 0 × 1 = 0 |
| 1 | 0 | 1 × 0 = 0 |
| 1 | 1 | 1 × 1 = 1 |
How to Multiply Binary Numbers?
The process of multiplying binary numbers is similar and easier to do than decimal multiplication as binary numbers consist of only two digits which are 0 and 1. The method of multiplying binary numbers is given below. The same set of rules also apply to binary numbers with a decimal point. Let us take the example of multiplying (\(11101)_{2}\) and (\(1001)_{2}\). The decimal equivalent of (\(11101)_{2}\) is 29 and the decimal equivalent of (\(1001)_{2}\) is 9. Now let us multiply these numbers.
Step 1: Write down the multiplicand (\(11101)_{2}\) and the multiplier (\(1001)_{2}\) one below the other in proper positions.
Step 2: Multiply the rightmost digit or the least significant bit (LSB) of the multiplier (1) with all the digits of the multiplicand (\(11101)_{2}\).
Step 3: Add a place holder of '0' or 'X' before multiplying the next higher order digit of the multiplier& with the multiplicand.
Step 4: Repeat the same process for all the next higher-order digits until we reach the most significant bit (MSB) which is the left-most digit of the multiplicand with the multiplier.
Step 5: The product obtained in each row is called the partial product. Finally, add all the partial products. To add all the binary numbers use the rules of binary addition.
(The rules for binary addition are listed as follows: 0 + 0 = 0, 0 + 1 = 1, and 1 + 1 = 0, with a carryover of 1. So, 1 + 1 = 10 and 1 + 1 + 1 = 11 in the binary number system)
Let us look at the following process of binary multiplication as described above.
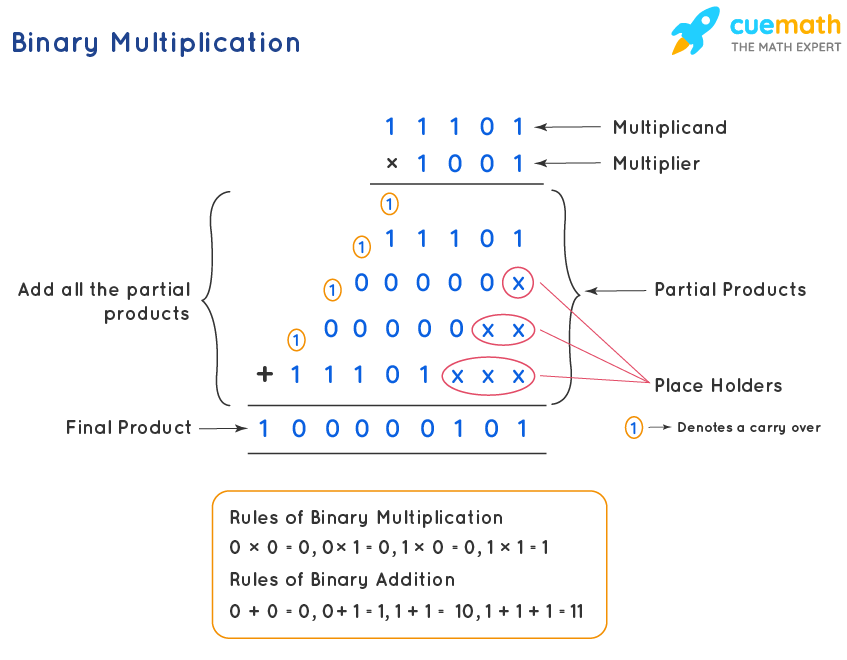
Therefore, the product of (\(11101)_{2}\) and (\(1001)_{2}\) is (\(100000101)_{2}\). Let us verify our answer. The decimal equivalent of (\(100000101)_{2}\) is 261. To know how to convert a binary number to a decimal number, click here. The decimal equivalent of& (\(11101)_{2}\) is 29 and the decimal equivalent of (\(1001)_{2}\) is 9. When we multiply 29 and 9 the product is 261. The decimal equivalent of (\(100000101)_{2}\) is 261. Hence, the product is correct.
Topics Related to Binary Multiplication
Check out some interesting topics related to binary multiplication.
Binary Multiplication Examples
-
Example 1: Using the binary multiplication rules, multiply (\(110)_{2}\) and (\(11)_{2}\).
Solution:
The rules for binary multiplication are:
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
Let us use the above rules to multiply the binary numbers.GIven, multiplicand = \(110_{2}\), multiplier = \(11_{2}\). We multiply the two numbers as shown below.

Therefore, the product of (\(110)_{2}\) and (\(11)_{2}\) is (\(10010)_{2}\). -
Example 2: Using the binary multiplication rules, find the product of (\(11011)_{2}\) and (\(101)_{2}\).
Solution:GIven multiplicand = (\(11011)_{2}\) and multiplier = (\(101)_{2}\)
On multiplying we get,
Therefore, the product of (\(11011)_{2}\) and (\(101)_{2}\) is (\(10000111)_{2}\).
-
Example 3: Using the binary multiplication rules, multiply the binary numbers (\(1011.1)_{2}\) and (\(10.1)_{2}\).
Solution:
Given multiplicand = (\(1011.1)_{2}\) and multiplier = (\(10.1)_{2}\).

Therefore, the product of (\(1011.1)_{2}\) and (\(10.1)_{2}\) is (\(11100.11)_{2}\)

FAQs on Binary Multiplication
What is Binary Multiplication?
Binary multiplication is the process of multiplying binary numbers. Binary numbers form the base-2 number system. Data is stored in a computer in the form of 0s and 1s. The process of multiplying binary numbers is the same as that of the arithmetic operation of multiplication which is done on decimal or base-10 numbers. The only difference is that binary numbers consist of 0s and 1s.
What are the Rules for Binary Multiplication?
Binary multiplication is also similar to multiplying base-10 numbers which are (0 to 9). Binary numbers comprise only 0s and 1s. Therefore, we need to know the product when 0 is multiplied with 0 and 1 and 1 is multiplied with 0 and 1. The rules for binary multiplication are as follows.
- 0 × 0 = 0
- 0 × 1 = 0
- 1 × 0 = 0
- 1 × 1 = 1
What is the Result of Binary Multiplication of (\(111)_{2}\) and (\(111)_{2}\)?
The product of (\(111)_{2}\) and (\(111)_{2}\) is (\(110001)_{2}\).
What are the Steps to do Binary Multiplication?
Binary multiplication of two numbers can be done by following the steps given below.
Step 1: Arrange the multiplier and the multiplicand in proper positions. For example, we may multiply a 3-digit number and a 2- digit number. In this case, the 2-digit number is to be placed correctly below the 3-digit number, like this,
110
× 10
--------
_____
Step 2: The next step is to multiply every digit of the multiplicand with every digit of the multiplier starting from the rightmost digit or the least significant bit (LSB). The product obtained after the multiplication of each digit of the multiplicand with the multiplier is called the partial product. Finally, we add the partial products obtained at each step using the rule of binary addition.
What is the Product of (\(1111)_{2}\) and (\(1111)_{2}\) Using Binary Multiplication?
The product of (\(1111)_{2}\) and (\(1111)_{2}\) using binary multiplication is (\(11100001)_{2}\). In this binary multiplication, the multiplier and the multiplicand are the same binary numbers. We use the rules of binary multiplication, which are ' 0 × 0 = 0, 1 × 0 = 0, 0 × 1 = 0& and 1 × 1 = 1', and multiply the numbers as per the usual arithmetic multiplication method.
What is Binary Multiplication of Negative Numbers?
In the decimal or the base-10 number system, there are negative numbers, such as -1, -2, -3, and so on. It is possible to multiply a negative number with a positive number or a negative number with a negative number in binary, as well. To do this, we represent each number using 8 bits. In this, we use 4 bits to represent the number in 2's complement and 4 bits to represent the sign. If the sign of the number is positive then we use four zeros and if the number is negative then we use fours ones. 2's complement of a binary number is obtained by adding 1 to the one's complement of the binary number. 1's complement means reversing every 0 with a 1 and every 1 with a 0.
What is the Result of Binary Multiplication of the Numbers (\(10100)_{2}\) and (\(01011)_{2}\)?
The product of (\(10100)_{2}\) and (\(01011)_{2}\) is (\(011011100)_{2}\).
visual curriculum