Exponential Growth And Decay
Exponential growth and decay apply to physical quantities which change in value or form in a rapid manner. The change can be measured using the concept of exponential growth and exponential decay, and the new obtained quantity can be obtained from the existing quantity. The formulas of exponential growth and decay are f(x) = a(1 + r)t, and f(x) = a(1 - r)t respectively.
Let us learn more about exponential growth and decay, the formula, applications, with the help of examples, FAQs.
What Is Exponential Growth And Decay?
Exponential growth and decay apply to quantities which change rapidly. Exponential growth and decay have been derived from the concept of geometric progression. Quantities that do not change as constant but change in an exponential manner can be termed as having an exponential growth or exponential decay.
The simplest representation of exponential growth and decay is the formula abx, where 'a' is the initial quantity, 'b' is the growth factor which is similar to the common ratio of the geometric progression, and 'x' in the time steps for multiplying the growth factor. For exponential growth, the value of b is greater than 1 (b > 1), and for exponential decay, the value of b is lesser than 1 (b < 1).
Exponential growth finds applications in studying bacterial growth, population increase, money growth schemes. Exponential decay refers to a rapid decrease in a quantity over a period of time. The exponential decay can be used to find food decay, half-life, radioactive decay. The formulas of exponential growth and decay are as presented below.
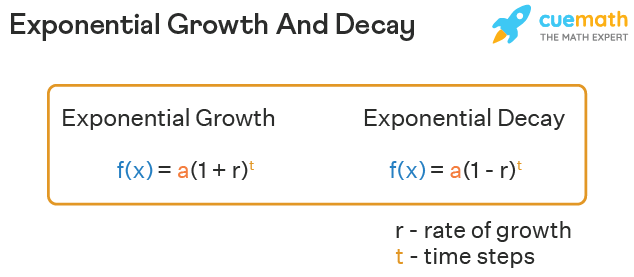
Exponential growth uses a factor 'r' which is the rate of growth. Here the r-value lies between 0 and 1 (0 < r < 1). The term (1 + r) can be taken as the growth factor. And 't' is the time steps which is the number of times the growth factor is to be multiplied. The value of 't' can be a whole number or a decimal number. For exponential decay, the growth factor is (1 - r), which has a value lesser than 1.
Formulas of Exponential Growth And Decay
The exponential growth and decay have different interpretations of the formulas which are interrelated and can be interpreted differently. The below table shows the three different formulas of exponential growth and decay.
| Exponential Growth | Exponential Decay |
|---|---|
| f(x) = abx | f(x) = ab-x |
| f(x) = a(1 + r)t | f(x) = a(1 - r)t |
| P = Poekt | P = Poe-kt |
In the above formulas the 'a' or Po is the initial quantity of the substance. Further for exponential growth b = 1 + r = ek and for exponential decay we have b = 1 - r = e-k.
Applications of Exponential Growth And Decay
The concept of exponential growth and decay can be observed in numerous day-to-day scientific and industrial activities. Let us check a few important applications of exponential growth and decay.
- Bacterial Growth: The initial bacterial growth can be observed in numerous communicable diseases. The recent Covid-19 is a quick example of exponential growth where the disease is highly communicable and is transmitted from one to many, and then to many more people. Bacteria and viruses are growing in an exponential manner, and the initial bacteria grows at an exponential rate. The initial bacterial if taken to double every second would grow in numbers such as 1, 2, 4, 8, 16, 32, 64, 128, 256, 512... With this, we can observe the manner of exponential growth in bacteria.
- Nuclear Chain Reactions: The nuclear chain reactions can be broadly classified as nuclear fission and nuclear fission reactions. The concept of nuclear fusion can be linked with exponential growth and the concept of nuclear fission can be linked with exponential decay. Nuclear fusion is a reaction in which two or more atoms combine to form a larger atom and this kind of reaction can be observed in the core of the sun. Nuclear fission is a kind of exponential decay that can be observed in radioactive material, in which the initial quantity decomposes and we have a smaller quantity by the end of the observed time period.
- Feedback: The concept of feedback, more so of customer feedback grows in an exponential manner. This can be observed more so in negative feedback. The bad functioning of the product if experienced by a customer is shared by this customer to another person, who in turn shares it with two or more people, and each of those people again shares it with two or more people. The medium of the internet helps for this easy sharing of feedback which flows exponentially to a larger customer segment. Thus the feedback in this current day of the internet is conveyed at a rapid pace.
- Processing Power of Computers: The processing and storage power has now increased exponentially. Earlier the data storage was only in MB, which has now grown to GB and TB exponentially. The slow growth in the computer hardware and storage system in the initial 1970s and 1980s has now grown exponentially. The initial floppy disks and hard disk drives have now been replaced with cloud servers which can be easily assessed by the user through an internet-connected mobile device.
- Food Degradation: Food degradation can also be understood as a case of exponent growth and decay. The food remains good for a certain amount of time and then it degenerates exponentially. The food is slightly stale initially, and then it stales rapidly until we discover that it has spoilt completely. This is also a typical case of exponential decay, where once the decay process initiates, then it decays at a rapid pace until the entire food quantity is completely stale.
- Aging of Human Beings: The aging process of humans or any living being at the ending part of the lifetime follows an exponential decay process. The person remains hale and healthy for a normal course of life for about 60 years. This is the same reason that for many jobs the retirement age is set as 60 years. After this, the aging process is so rapid that it affects the body at an exponential rate. The degradation in the quality of life seen in the initial days is further degraded drastically in the later years. This could be because of the advancement of certain existing diseases or the malfunctioning of certain organs.
- Internet Content: The internet is exploding with information. In the initial stages of the internet, google had to collect useful information and add it to the net. But with time the internet users started adding information to the internet, and now the amount of information now available on the internet is mind-boggling. Also now the application of artificial intelligence algorithms helps build the content in an exponential manner. The content is generated thousands and millions of times in a short span of time.
☛Related Topics
FAQs on Exponential Growth And Decay
What Is Exponential Growth And Decay In Maths?
Exponential growth and decay in maths applies to the calculation of rapidly changing quantity. There are numerous quantities and values in nature, industry, business which change rapidly with time. Compound internet, decpreciation, growth of virus, spoiling of perishable foods, are some of the real life examples which need to be calculated using a math formula. The exponential growth and decay gives the required needed calculations using the formulas f(x) = a(1 + r)t, and f(x) = a(1 - r)t. Here a is the initial quantity, r is the growth or decay constant, and t is the time period or the time factor.
What Is The Formula For Exponential Growth And Decay?
There are three types of formulas that are used for computing exponential growth and decay. The three formulas are as follows.
- f(x) = abx for exponential growth and f(x) = ab-x for exponential decay. Here 'a' is the initial quantity, 'b' is the growth or decay factor, and 'x' is the time step.
- f(x) = a(1 + r)t, and f(x) = a(1 - r)t are for exponential growth and exponential decay respectively. Here 'r' is the growth or decay factor and has a value between 0 and 1, (0 < r < 1).
- P = Poekt, P = Poe-kt are for formulas of exponential growth and decay. Here Po is the initial quantity, P is the obtained quantity, e is the exponential factor, and k is the growth or decay constant.
What Is The Difference Between Exponential Growth And Exponential Decay?
Exponential growth refers to an increase of the resultant quantity for a given quantity, and exponential decay refers to the decrease of the resultant quantity for a given quantity. The exponential growth and decay both need the initial quantity, the time period and the decay or growth constant to find the resultant quantity. Exponetial growth finds use in finance, medicine, biology, and exponential decay find use to find the depreciation of an asset, to find the expiry date of a manufactured item.
What Is The Use Of Exponential Growth And Decay In Maths?
The exponential growth and decay can be used to calculate the resultant quantity after a process of exponential growth or exponetial decay. From the given initial quantity, and the rate of growth or decay we can easily compute the resultant quantity. We can calculate the exponent growth and decay using f(x) = a(1 + r)t, and f(x) = a(1 - r)t.
What Are The Applications Of Exponential Growth And Decay In Daily Life?
The exponential growth and decay have numerous applications in our day-to-day life. The biological world has numerous examples of diseases and their spread, micro organisms, virus and their growth, which needs to be computed. Further we find numerous examples of exponential growth in finance, business, the internet, consumer behavior.