Sin Cos Tan Formulas
Before going to learn the sin, cos, tan formulas, let us recall what are sin, cos, and tan. These are three of the six trigonometric ratios which are considered to be the primary functions while solving trigonometric problems. These trigonometric ratios are used to calculate the sides of a right triangle. The three other major trigonometric ratios apart from sin, cos and tan are cot, sec, and cosec. Let's look into the sin, cos, tan formulas in detail.
What Are Sin Cos Tan Formulas?
The sin cos tan formulas are defined for a right triangle. Let us consider a right triangle ABC that is right angled at C. Then AB is the longest side and hence it is called the hypotenuse. AC and BC are the sides that are adjacent and opposite to the angle A respectively. The trigonometric ratios sin, cos, and tan for the angle A are as follows.
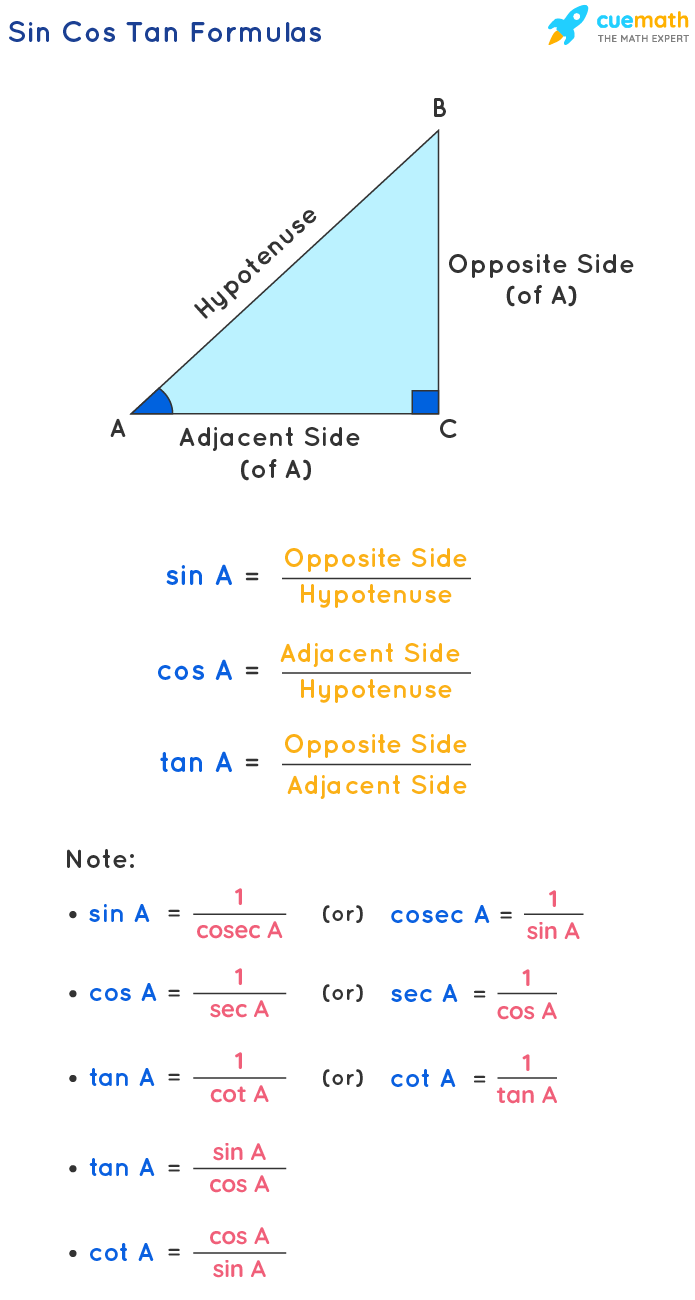
Sin Cos Tan Formulas
The important sin cos tan formulas (with respect to the above figure) are:
- sin A = Opposite side/Hypotenuse = BC/AB
- cos A = Adjacent side/Hypotenuse = AC/AB
- tan A = Opposite side/Adjacent side = BC/AC
We can derive some other sin cos tan formulas using these definitions of sin, cos, and tan functions. We know that sin, cos, and tan are the reciprocals of cosec (or csc), sec, and cot functions. Thus, we can derive 3 more formulas related to sin, cos, and tan.
- sin A = 1/csc A (or) csc A = 1/ sin A
- cos A = 1/sec A (or) sec A = 1/cos A
- tan A = 1/cot A (or) cot A = 1/tan A
The functions tan and cot can be expressed in terms of sin and cos as well using the sin, cos, and tan formulas.
sin A/cosA = (Opposite side/Hypotenuse) / (Adjacent side/Hypotenuse)
= Opposite side/Adjacent side
= tan A
Similarly,
cos A/sin A = (Adjacent side/Hypotenuse) / (Opposite side/Hypotenuse)
= Adjacent side/Opposite side
= cot A
Thus, the two formulas that connect tan and cot with sin and cos are:
- tan A = sin A/cos A
- cot A = cos A/sin A

Let us see the applications of the sin cos tan formulas in the section below.
Examples Using Sin Cos Tan Formulas
Example 1: Using the triangle below, find the value of sin A, cos A, and tan A. using sin cos tan formulas.
 .
.
Solution:
Using sin cos tan formulas,
Sin A = Side opposite to angle A / Hypotenuse
= BC/AB
= 5/13
Cos A = Side adjacent to angle A / Hypotenuse
= AC/AB
= 12/13
tan A = Opposite side/Adjacent side
= BC/AC
= 5/12
Answer: sin A = 5/13, cos A = 12/13, and tan A = 5/12.
Example 2: If sin A = 6/10 and cos A = 8/10, calculate tan A.
Solution:
Using sin cos tan formulas,
tan A = sin A / cos A
= (6/10) / (8/10)
= 6/8
= 3/4
Answer: tan A = 3/4.
Example 3: If csc A = 5/3 and sec A = 5/4, find the value of tan A.
Solution:
Using sin cos tan formulas,
sin A = 1/csc A = 1 / (5/3) = 3/5
cos A = 1/sec A = 1 / (5/4) = 4/5
tan A = sin A / cos A
= (3/5) / (4/5)
= 3/4
Answer: tan A = 3/4.
FAQs on Sin Cos Tan Formulas
What Are Sin Cos Tan Formulas?
The sin cos tan formulas are nothing but the definitions of the sine function, cosine function, and the tangent function. The sin cos tan formulas are:
- sin A = Opposite side/Hypotenuse
- cos A = Adjacent side/Hypotenuse
- tan A = Opposite side/Adjacent side
What Is the Easy Way To Remember the Sin Cos Tan Formulas?
The sin cos tan formulas can be remembered using SOH CAH TOA. It means that Sine is Opposite over the Hypotenuse, Cosine is Adjacent over Hypotenuse, and Tan is Opposite over Adjacent.
What Are the Applications of Sin Cos Tan Formulas?
The sin cos tan formulas are mainly used in finding the unknown lengths of a right-angled triangle. These are commonly used in solving height and distance problems.
How To Know What Sin Cos Tan Formula Should Be Used?
We will use the relevant sin cos tan formula depending on the available information. For example, in a right triangle, if we know, one angle, and its opposite side, and if we want to find the hypotenuse, we apply the sin formula to that reference angle which is sin θ = opposite/hypotenuse.
visual curriculum