Sin 870 Degrees

The value of sin 870 degrees is 0.5. Sin 870 degrees in radians is written as sin (870° × π/180°), i.e., sin (29π/6) or sin (15.184364. . .). In this article, we will discuss the methods to find the value of sin 870 degrees with examples.

• Sin 870°: 0.5
• Sin 870° in fraction: 1/2
• Sin (-870 degrees): -0.5
• Sin 870° in radians: sin (29π/6) or sin (15.1843644 . . .)

What is the Value of Sin 870 Degrees?

The value of sin 870 degrees in decimal is 0.5. Sin 870 degrees can also be expressed using the equivalent of the given angle (870 degrees) in radians (15.18436 . . .).

We know, using degree to radian conversion, θ in radians = θ in degrees × (pi/180°)
⇒ 870 degrees = 870° × (π/180°) rad = 29π/6 or 15.1843 . . .
∴ sin 870° = sin(15.1843) = 1/2 or 0.5

Explanation:

For sin 870°, the angle 870° > 360°. Given the periodic property of the sine function, we can represent it as sin(870° mod 360°) = sin(150°). The angle 870°, coterminal to angle 150°, is located in the Second Quadrant(Quadrant II).
Since sine function is positive in the 2nd quadrant, thus sin 870 degrees value = 1/2 or 0.5
Similarly, sin 870° can also be written as, sin 870 degrees = (870° + n × 360°), n ∈ Z.
⇒ sin 870° = sin 1230° = sin 1590°, and so on.
Note: Since, sine is an odd function, the value of sin(-870°) = -sin(870°).

Methods to Find Value of Sin 870 Degrees

The sine function is positive in the 2nd quadrant. The value of sin 870° is given as 0.5. We can find the value of sin 870 degrees by:

• Using Trigonometric Functions
• Using Unit Circle

Sin 870° in Terms of Trigonometric Functions

Using trigonometry formulas, we can represent the sin 870 degrees as:

• ± √(1-cos²(870°))
• ± tan 870°/√(1 + tan²(870°))
• ± 1/√(1 + cot²(870°))
• ± √(sec²(870°) - 1)/sec 870°
• 1/cosec 870°

Note: Since 870° lies in the 2nd Quadrant, the final value of sin 870° will be positive.

We can use trigonometric identities to represent sin 870° as,

• sin(180° - 870°) = sin(-690°)
• -sin(180° + 870°) = -sin 1050°
• cos(90° - 870°) = cos(-780°)
• -cos(90° + 870°) = -cos 960°

Sin 870 Degrees Using Unit Circle

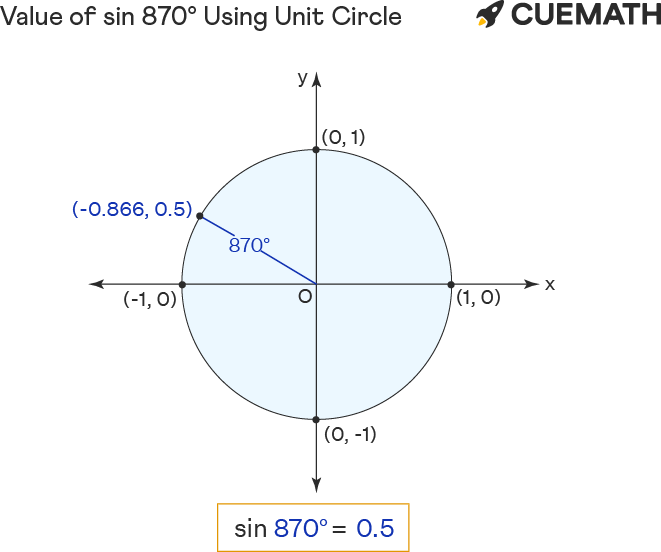
To find the value of sin 870 degrees using the unit circle, represent 870° in the form (2 × 360°) + 150° [∵ 870°>360°] ∵ sine is a periodic function, sin 870° = sin 150°.

• Rotate ‘r’ anticlockwise to form 150° or 870° angle with the positive x-axis.
• The sin of 870 degrees equals the y-coordinate(0.5) of the point of intersection (-0.866, 0.5) of unit circle and r.

Hence the value of sin 870° = y = 0.5

☛ Also Check:

• sin 104 degrees
• sin 20 degrees
• sin 90 degrees
• sin 68 degrees
• sin 33 degrees
• sin 405 degrees

FAQs on Sin 870 Degrees

What is Sin 870 Degrees?

Sin 870 degrees is the value of sine trigonometric function for an angle equal to 870 degrees. The value of sin 870° is 1/2 or 0.5.

What is the Value of Sin 870° in Terms of Cosec 870°?

Since the cosecant function is the reciprocal of the sine function, we can write sin 870° as 1/cosec(870°). The value of cosec 870° is equal to 2.

What is the Value of Sin 870 Degrees in Terms of Cos 870°?

Using trigonometric identities, we can write sin 870° in terms of cos 870° as, sin(870°) = √(1-cos²(870°)). Here, the value of cos 870° is equal to -0.8660254.

How to Find the Value of Sin 870 Degrees?

The value of sin 870 degrees can be calculated by constructing an angle of 870° with the x-axis, and then finding the coordinates of the corresponding point (-0.866, 0.5) on the unit circle. The value of sin 870° is equal to the y-coordinate (0.5). ∴ sin 870° = 0.5.

How to Find Sin 870° in Terms of Other Trigonometric Functions?

Using trigonometry formula, the value of sin 870° can be given in terms of other trigonometric functions as:

• ± √(1-cos²(870°))
• ± tan 870°/√(1 + tan²(870°))
• ± 1/√(1 + cot²(870°))
• ± √(sec²(870°) - 1)/sec 870°
• 1/cosec 870°

☛ Also check: trigonometric table