Equal Sets
Equal sets are sets in set theory in which the number of elements is the same and all elements are equal. It is a concept of set equality. Before getting into the detail of the concept of equal sets, let us recall the meaning of sets. A set is a well-defined collection of objects such as letters, numbers, people, shapes, etc. They are generally denoted by a capital letter and braces '{}'.
We study different types of sets in set theory. In this article, we will explore the concept of equal sets, its definition, and their properties. We will also understand the difference between equal sets and equivalent sets with the help of examples for a better understanding.
| 1. | What are Equal Sets? |
| 2. | Equal Sets Definition |
| 3. | Properties of Equal Sets |
| 4. | Difference Between Equal and Equivalent Sets |
| 5. | FAQs on Equal Sets |
What are Equal Sets?
Equal sets are defined as the sets that have the same cardinality and all equal elements. In other words, two or more sets are said to be equal sets if they have the same elements and the same number of elements. For example set A = {1, 2, 3, 4, 5} and B = {1, 2, 3, 4, 5}. Then sets A and B are said to be equal sets as their elements are the same and they have the same cardinality.
Now, two sets are said to be unequal sets if all the elements are not the same in two sets, and sets that have the same number of elements are called equivalent sets. For example, if A = {1, 2, 3, 4, 5}, C = {2, 4, 6, 7, 9}, and D = {2, 5, 6} . Sets A and C have the same number of elements but all the elements are not equal. Therefore, A and C are equivalent sets. Now, sets A and D do not have the same cardinality and the elements are also not equal. Therefore, sets A and D are unequal sets. The equal and equivalent sets can be understood from the number of elements and the similarity of elements of the two sets.
Equal Sets Definition
If all elements of two or more sets are equal and the number of elements is also equal, then the sets are said to be equal sets. The notation used to denote equal sets is '=', i.e., if sets A and B are equal, then it is written A = B. We know that the order of elements in sets does not matter. So, if A = {a, b, c, d} and B = {b, a, d, c}, then A and B are equal sets because they have the same elements, and order of the elements does not impact the equality of the sets.
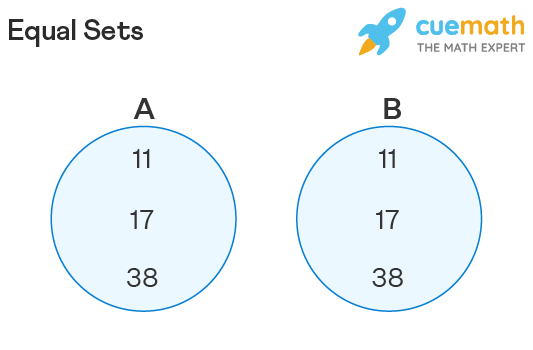
Equal Sets Representation Using Venn Diagram
Let us now represent equal sets on a Venn diagram. The Venn diagram given below shows two equal sets A and B with the same number of elements and equal elements, i.e., A = {11, 17, 38} = B.
Properties of Equal Sets
Now, we have understood the meaning of equal sets. Next, we will study some of its important properties that help in understanding and identifying them:
- The order of the elements does not impact the equality of the two sets.
- Equal sets have the same cardinality, that is, they have the same number of elements.
- If two sets are subsets of each other, then the set notation used is A ⊆ B and B ⊆ A, and the two sets are equal. A = B.
- Equal sets must have all equal elements.
- The power set of equal sets also has the same cardinal number.
- Equal and equivalent sets have the same property of equal number of elements.
- All equal sets are equivalent sets but the converse is not true.
Difference Between Equal And Equivalent Sets
The table given below highlights the similarities and differences between equal and equivalent sets:
| Equal Sets | Equivalent Sets |
|---|---|
| If all elements are equal in two or more sets, then they are equal. | If the number of elements is the same in two or more sets, then are equivalent. |
| Equal sets have the same cardinality | Equivalent sets have the same cardinality. |
| They have the same number of elements. | They have the same number of elements. |
| The symbol used to denote equal sets is '=' | The symbol used to denote equivalent sets is ~ or ≡ |
| All equal sets are equivalent sets. | Equivalent sets may or may not be equal. |
| Elements should be the same. | Elements need not be the same. |
Important Properties of Equal Sets
- Equal sets are equivalent but equivalent sets need not be equal.
- Sets with the same elements are equal.
- If two sets are subsets of each other, then they are equal.
Related Topics
FAQs on Equal Sets
What are Equal Sets in Math?
Equal sets are sets in math in which the number of elements is the same and all elements are equal. Equal sets are defined as the sets that have the same cardinality and all equal elements.
What is the Difference Between Equal And Equivalent Sets?
The difference between equal and equivalent sets is only in the difference of the elements. If all elements are equal in two or more sets, then they are equal but in equivalent sets, the elements need not be the same but the number of elements should be the same.
How to Identify Equal Sets?
To identify equal sets, all elements of the sets should be equal and the number of elements should be the same.
How to Prove that Two Sets are Equal?
To prove two sets are equal, we can prove them to be subsets of each other. Another way to show equal sets, we can check the equality of the elements and their cardinality.
What are Equal and Unequal Sets?
Two or more sets are said to be equal sets if they have the same elements and the same number of elements. If any of these conditions is not satisfied, then the sets are unequal, that is, if the sets are not equal, then. they are said to be unequal sets.
Are Equivalent Sets Equal Sets?
All equivalent sets are not equal sets. Equivalent sets are equal only if all the elements of the sets are equal.
What is the Set Notation Used for Equal Sets?
The symbol used to represent equal sets is '='. The set notation used to represent set A and set B, which are equal is A = B.