Volume of a Right Square Pyramid
The volume of a right square pyramid is the space occupied by the right square pyramid. A right square pyramid is a three-dimensional geometric shape that has a right square base and four triangular faces that are joined at a vertex. Let's learn how to find the volume of a right square pyramid with the help of a few solved examples and practice questions.
| 1. | What is Volume of a Right Square Pyramid? |
| 2. | Formula of Volume of a Right Square Pyramid |
| 3. | How to Find the Volume of a Right Square Pyramid? |
| 4. | FAQs on Right Square Pyramid Volume |
What is Volume of a Right Square Pyramid?
The volume of a right square pyramid is the number of unit cubes that can fit into it. A right square pyramid is a three-dimensional shape that has a right square base and four triangular faces that are joined at a vertex. A right square pyramid is a polyhedron (pentahedron) with five faces. The unit of volume is "cubic units". For example, it can be expressed as m3, cm3, in3, etc depending upon the given units.

A right square pyramid has three components.
- The top point of the pyramid is called the apex.
- The bottom right square is called the base.
- The triangular sides are called faces.
Formula of Volume of a Right Square Pyramid
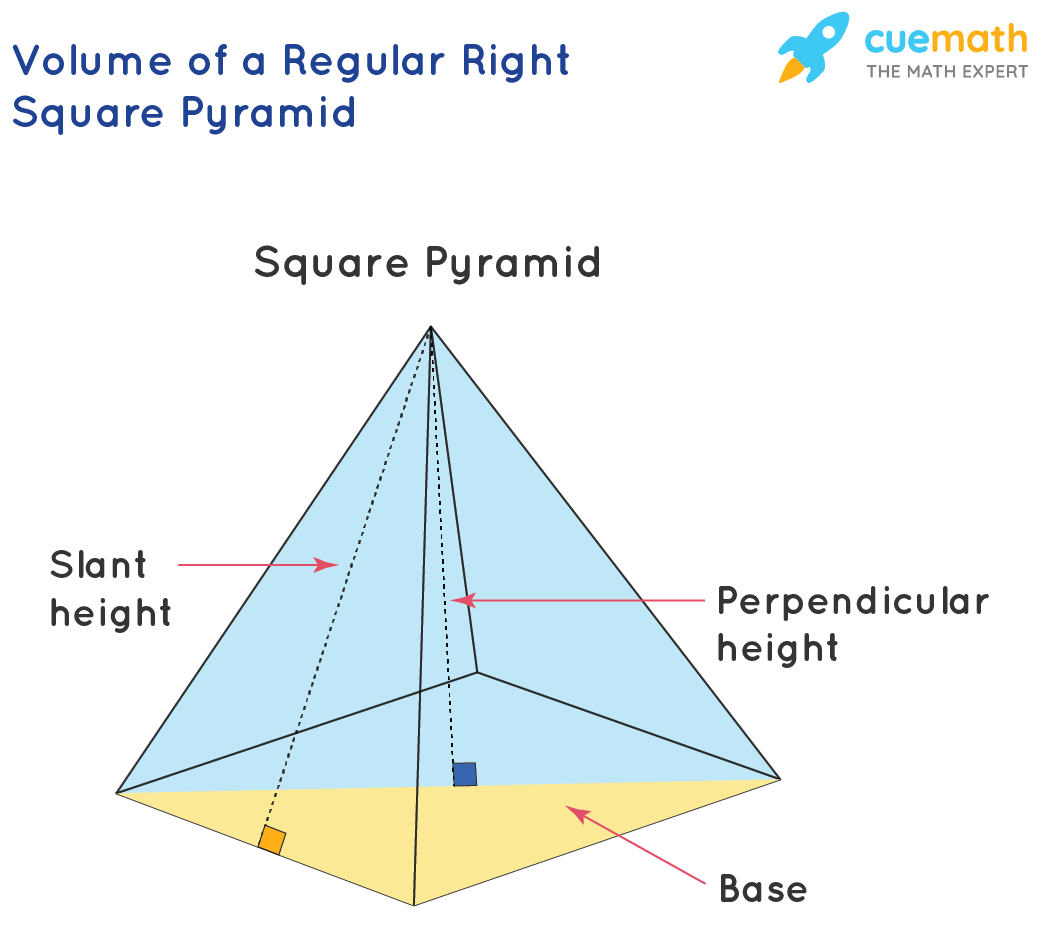
The formula to determine the volume of a right square pyramid is V = 1/3 × b2 × h where "b" is the length of the base and "h" is the perpendicular height. The relation between slant height, perpendicular height, and the base is given by using Pythagoras Theorem s2 = h2 + (b/2)2 where "s", "h" and "b" are slant height, the height of perpendicular, and base length of the right square pyramid, respectively. Thus, the volume of the right square pyramid is given by replacing the given dimensions in the formula V = 1/3 × b2 × h.
How to Find the Volume of a Right Square Pyramid?
As we learned in the previous section, the volume of a right square pyramid could be found using \(\dfrac{1}{3} \times \text{b}^2 \times \text{h}\). Thus, we follow the below steps to find the volume of a right square pyramid.
- Step 1: Determine the base area (b2) and the height (h) of the pyramid.
- Step 2: Find the volume using the formula 1/3 × b2 × h
- Step 3: Represent the final answer with cubic units.
Example: Find the volume of the right square pyramid having height and length of the base edge of 9 units and 5 units respectively.
Solution: Given that h = 9 units and b = 5 units.
Then, the volume of the right square pyramid is V = 1/3 × b2 × h
⇒ V = 1/3 × 52 × 9
⇒ V = 52 × 3 = 75 cubic units
Answer: The volume of the right square pyramid is 75 cubic units.
Solved Examples on Volume of a Right Square Pyramid
-
Example 1: Julia has a vessel in the form of an inverted regular right square pyramid that has to be filled with water. The altitude of the vessel is 10 inches and the length of the base edge is 7 inches. What is the volume of water Julia can fill in the vessel?
Solution: Given h = 10 inches and b = 7 inches
The volume of the vessel is given by V = 1/3 × b2 × h
⇒ V = 1/3 × 72 × 10
⇒ V = 490/3
⇒ V = 163.33 cubic inches
Answer: Thus, the volume of the vessel is 163.33 in3. -
Example 2: What will be the volume of a regular square pyramid with base sides 10 cm and a height of 18 cm?
Solution: Given that b = 10 cm and h = 18 cm
The formula for the volume of a square pyramid is given by V = 1/3 × b2 × h
The area of the base = The square of base length = 102 or 100 cm2.
Putting the values b2 = 100 and h = 18 in the formula.V = 1/3 × 100 × 18 = 600 cm3.
Answer: The volume of the right square pyramid is 600 cm3.

FAQs on Volume of a Right Square Pyramid
What is the Volume of a Right Square Pyramid?
The volume of a right square pyramid is defined as the number of unit cubes that can fit into a right square pyramid. A right square pyramid is a three-dimensional geometric shape that has a right square base and four triangular faces that are joined at a vertex.
What Units Are Used With the Volume of the Right Square Pyramid?
The unit used with the volume of the right square pyramid is given in cubic units. For example, m3, cm3, in3, etc depending upon the given units.
What is the Formula of the Volume of the Right Square Pyramid?
The formula of the volume of the right square pyramid is given as V = 1/3 × Base Area × Height = 1/3 × b2 × h where b2 shows the base area and h shows the height of the right square pyramid.
How to Find the Volume of a Right Square Pyramid?
The volume (V) of a right square pyramid can be found by using the following steps:
- Step 1: Find the base area (b2) and the height (h) of the pyramid.
- Step 2: Determine the volume using the formula 1/3 × b2 × h
- Step 3: Now, write the final answer with cubic units.
How to Find the Volume of a Right Square Pyramid with Slant Height?
The volume (V) of a right square pyramid can be found by using the following steps:
- Step 1: Identify the given dimensions of the right square pyramid.
- Step 2: Find the missing dimension using the formula s2 = h2 + (b/2)2 where "s", "h", and "b" are slant height, the height of perpendicular, and base length of the right square pyramid, respectively.
- Step 2: Determine the volume using the formula V = 1/3 × b2 × h
- Step 3: Now, write the final answer with cubic units.
What Happens to the Volume of a Right Square Pyramid If the Height of the Pyramid is Doubled?
The volume of the right square pyramid is doubled if the height of the pyramid is doubled as "h". In the formula, V = 1/3 × b2 × h, substitute height = 2h, V = 1/3 × b2 × (2h) = 2 × (1/3 × b2 × h) which gives double the volume of the original volume of the right square pyramid.
What Happens to the Volume of a Right Square Pyramid If the Base of the Pyramid is Halved?
The volume of the right square pyramid becomes one-fourth the original volume if the base of the pyramid is halved as "b/2". In the formula, V = 1/3 × b2 × h, substitute base edge = b/2, V = 1/3 × (b/2)2 × h = (1/4) × (1/3 × b2 × h) which gives one fourth the volume of the original volume of the right square pyramid.
visual curriculum