Volume of Slanted Cylinder
The volume of a slant cylinder is the amount of liquid that can be held by a slanted cylinder. A cylinder is a three-dimensional solid figure which consists of two circular bases connected with a curved face and the curved face is sitting upright to the base making a right angle with the base plane. But a slanted cylinder is a titled cylinder where a curved surface makes any angle but 90 degrees with the base. The volume of this slanted cylinder can be calculated by multiplying its base area with the height of the cylinder. A slanted cylinder is also known as an oblique cylinder or tilted cylinder. Here in this topic, we will discuss what is the volume of the slanted cylinder and how to calculate it along with solved examples and practice questions.
| 1. | What is the Volume of Slanted Cylinder? |
| 2. | Formula of Volume of Slanted Cylinder |
| 3. | How to Find the Volume of Slanted Cylinder? |
| 4. | FAQs on Volume of Slanted Cylinder |
What Is the Volume of Slanted Cylinder?
The volume of a slanted cylinder is nothing but the same volume as the volume of the right circular cylinder of the same height. We know the volume of right circular cylinder is the product of the base area of a cylinder and the height of the cylinder. The base area of a general cylinder is actually an area of a circle since the base of the cylinder is a circle and the volume can be simply found out by multiplying this area by its height. The volume of an oblique or slanted cylinder is measured in cubic units, for example - m3, cm3, in3, etc.
So, the volume of the slanted cylinder is V = Base area of cylinder × Height of cylinder
⇒ V = (π × radius2) × h
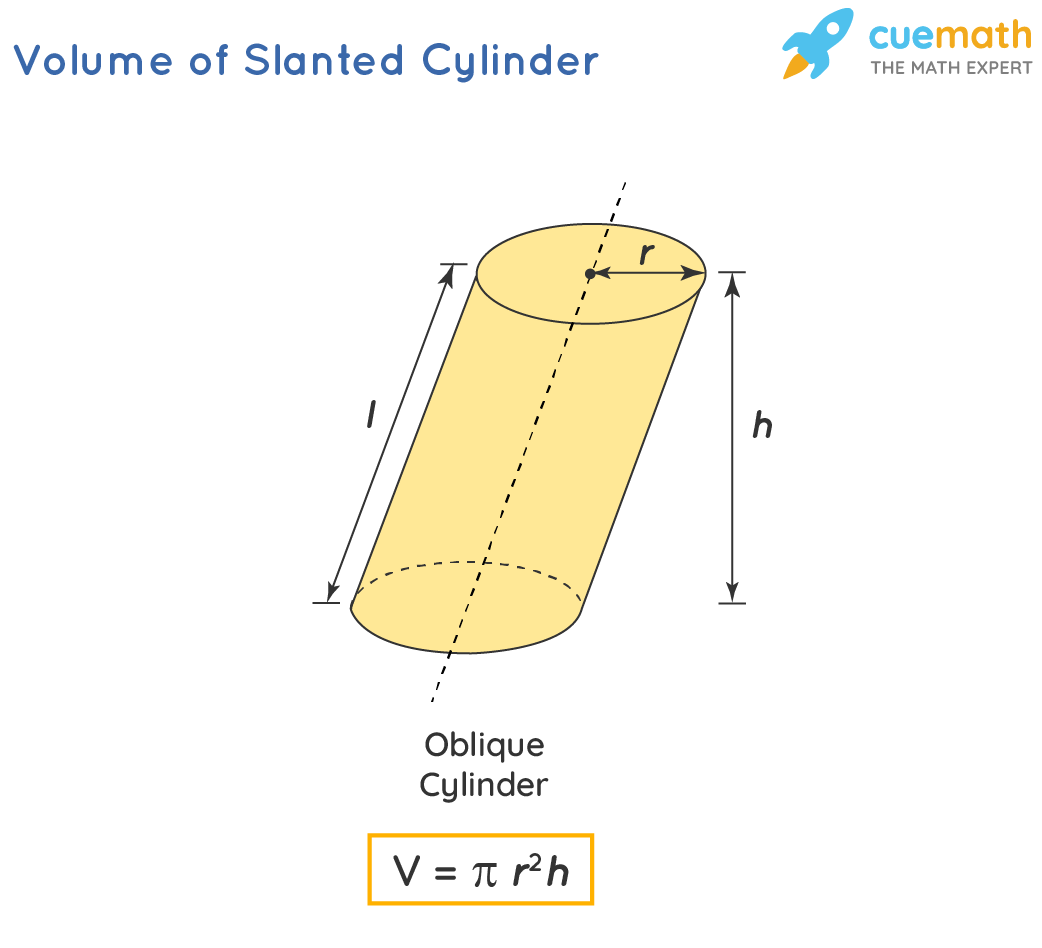
The Volume of a Slanted Cylinder Formula
The formula of the volume of the slanted cylinder is used to find the volume of the slanted cylinder. The volume of cylinder is obtained by multiplying the area of the base with the height of the slanted cylinder. Thus, the formula for the volume of the slanted cylinder, with a radius is r is "πr2h".
The volume of a slanted cylinder = (π × radius2 × h) cubic units.
How To Find the Volume of Slanted Cylinder?
The volume of a titled or slanted cylinder can be calculated by following the given steps:
- Step 1: Identify the radius of the base of the cylinder.
- Step 2: Find out the product of the square of its radius to π.
- Step 3: Find the height of the cylinder. If slant height (l) is known, use the following formula to calculate the height: h = √(l2 - r2) where r is the radius of the circular base.
- Step 4: Find the product of the base area and the height.
- Step 5: Give your answer in cubic units.
Example: Find the volume of a slanted cylinder whose radius is 7 inches and height is 21 inches. (Use π = 22/7)
Solution: Given that r = 7 inches and h = 21 inches
We know that volume of a slanted cylinder, V = πr2h cubic inches
⇒ V = (22/7) × (72) × 21
⇒ V = 22 × 7 × 21
⇒ V = 3234 cubic inches
Thus, the volume of the slanted cylinder is 3234 cubic inches.
Examples on Volume of a Slanted Cylinder
-
Example 1: The radius of a slanted cylinder is 5 inches. Find the volume of the cylinder if the slant height of the cylinder is 13 inches.
Solution: Given that r = 5 in and l = 13in
Area of the base is A = πr2
A = π × 5 × 5
⇒ A = 25 π
⇒ A = 78.539 square inchesThe height of the cylinder is given as h = √(l2 - r2)
⇒ h = √(132 - 52)
⇒ h = √144 = 12 inchesThe volume of the slanted cylinder, V = Base area × Height
V = 78.539 × 12
⇒ V = 942.477 cubic inchesTherefore, the volume of the slanted cylinder is 942.477 cubic inches.
-
Example 2: Walter has given a slanted cylinder of volume 576 π cubic units. Find the radius of the base of the circle if the height of the cylinder is 16 units.
Solution: Given that V = 576π cubic units and h = 16 units
Using the formula of Volume of cylinder V = πr2h
576π = π × r2× 16
⇒ 576 = r2× 16
⇒ r2 = 36
⇒ r = 6Therefore, the radius of the cylinder is 6 units.

FAQs on the Volume of Slanted Cylinder
What is the Volume of Slanted Cylinder?
The volume of the slanted cylinder is the amount of liquid it can hold within it. A slanted cylinder is also referred to as an oblique or tilted cylinder. The unit of volume of the slanted cylinder is given in cubic units for example - m3, cm3, in3, etc.
What is the Formula of Volume of Slanted Cylinder?
The formula of the volume of the slanted cylinder is given as V = πr2h where "V", "r", and "h" are volume, radius, and height of the cylinder. This formula shows the dependence of the volume of the slanted cylinder in terms of radius and height of the cylinder. However, we can find the volume of the slanted cylinder if its slant height is given using the formula h = √(l2 - r2) obtained by using the Pythagoras theorem.
How to Find Volume of Slanted Cylinder?
We can find the volume of the slanted cylinder using the following steps:
- Step 1: Identify the radius of the cylinder.
- Step 2: Determine the product of the square of radius and π.
- Step 3: Identify the height of the cylinder.
- Step 4: Now, find the product of the base area and the height.
- Step 5: Write the obtained answer in cubic units.
How to Find the Volume of Slanted Cylinder with Base Area of Cylinder?
We can find the volume of the slanted cylinder with the base area of the cylinder using the following steps:
- Step 1: Identify the base area and height of the cylinder.
- Step 2: Determine the product of the base area of the cylinder and the height of the cylinder.
- Step 3: The obtained answer is given in cubic units.
How to Find the Volume of Slanted Cylinder with Slant Height?
We can find the volume of the slanted cylinder with slant height using the following steps:
- Step 1: Identify the radius of the base of the cylinder.
- Step 2: Find out the product of the square of its radius to π.
- Step 3: Use the formula to calculate the height, h = √(l2 - r2) where r is the radius of the circular base.
- Step 4: Now, find the product of the base area and the height.
- Step 5: Give the obtained answer in cubic units.
What Happens to the Volume of Slanted Cylinder If the Base Radius is Doubled?
The volume of the slanted cylinder is quadrupled if the base radius is doubled as "r" is substituted by "2r" in the formula of volume, V = πr2h = π(2r)2h = 4(πr2h) which gives four times the original volume of the slant cylinder.
What Happens to the Volume of Slanted Cylinder If the Height of Cylinder is Tripled?
The volume of the slanted cylinder is thrice its original volume if the height of the cylinder is tripled as "h" is substituted by "3h" in the formula of volume, V = πr2h = πr2(3h) = 3(πr2h) which gives three times the original volume of the slant cylinder.
visual curriculum