Volume of Cylinder
The volume of a cylinder is the capacity of the cylinder which calculates the amount of material quantity it can hold. In geometry, there is a specific formula to calculate the volume of a cylinder that is used to measure how much amount of any quantity whether liquid or solid can be immersed in it uniformly. A cylinder is a three-dimensional shape with two congruent and parallel identical bases. There are different types of cylinders. They are:
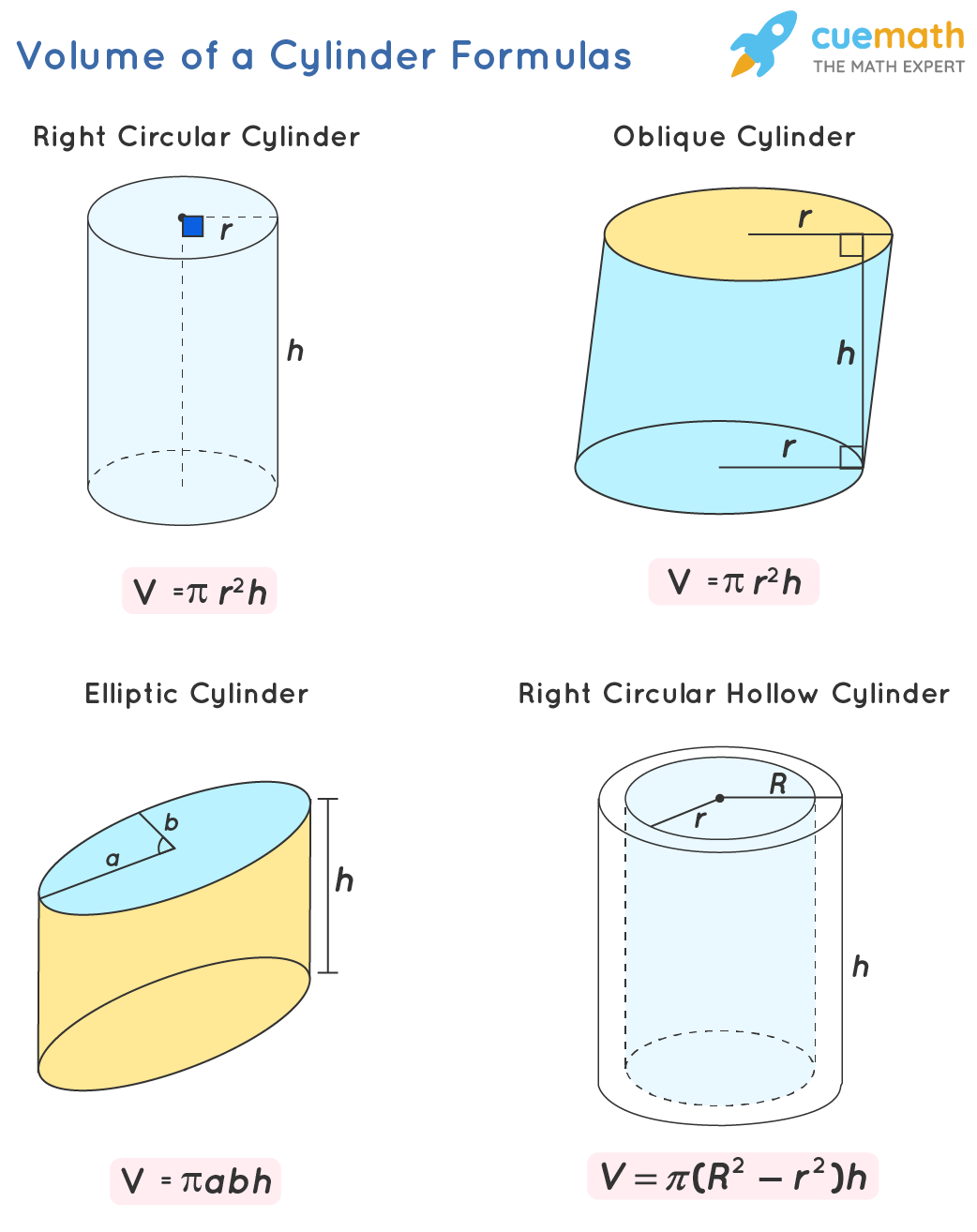
- Right circular cylinder: A cylinder whose bases are circles and each line segment that is a part of the lateral curved surface is perpendicular to the bases.
- Oblique Cylinder: A cylinder whose sides lean over the base at an angle that is not equal to a right angle.
- Elliptic Cylinder: A cylinder whose bases are ellipses.
- Right circular hollow cylinder: A cylinder that consists of two right circular cylinders bounded one inside the other.
The formula to find the volume of a cylinder is V = πr2h. Let us learn more about this formula in the upcoming sections.
| 1. | Volume of a Cylinder |
| 2. | Volume of a Cylinder Formula |
| 3. | How To Find the Volume of a Cylinder? |
| 4. | FAQs on Volume of a Cylinder |
What is the Volume of a Cylinder?
The volume of a cylinder is the number of unit cubes (cubes of unit length) that can be fit into it. It is the space occupied by the cylinder as the volume of any three-dimensional shape is the space occupied by it. The volume of a cylinder is measured in cubic units such as cm3, m3, in3, etc. Let us see the formula used to calculate the volume of a cylinder.
Definition of a Cylinder
A cylinder is a three-dimensional solid shape that consists of two parallel bases linked by a curved surface. These bases are like a circular disk in a shape. The line passing from the center or joining the centers of two circular bases is called the axis of the cylinder.
Volume of Cylinder Formula
We know that a cylinder resembles a prism (but note that a cylinder is not a prism as it has a curved side face), we use the same formula of volume of a prism to calculate the volume of a cylinder as well. We know that the volume of a prism is calculated using the formula,
V = A × h, where
- A = area of the base
- h = height
Using this formula, the formulas of volume of cylinder are:
- The formula for volume of a right circular cylinder is, V = πr2h (r = radius, h = height)
- The formula for volume of an oblique cylinder is, V = πr2h (r = radius, h = height)
- The formula for volume of an elliptic cylinder is, V = πabh (a and b = radii, h = height)
- The formula for volume of a right circular hollow cylinder is, V = π(R2 - r2)h (R = outer radius, r = inner radius, h = height)
Now we will apply the formula V = A × h to calculate the volume of different types of cylinders.
Volume of a Right Circular Cylinder Formula
We know that the base of a right circular cylinder is a circle and the area of a circle of radius 'r' is πr2. Thus, the volume (V) of a right circular cylinder, using the above formula (V = A × h), is,
V = πr2h
Here,
- 'r' is the radius of the base (circle) of the cylinder
- 'h' is the height of the cylinder
- π is a constant whose value is either 22/7 (or) 3.142.
Thus, the volume of cylinder directly varies with its height and directly varies with the square of its radius. i.e., if the radius of the cylinder becomes double, then its volume becomes four times.
Formula to Find Volume of an Oblique Cylinder
The formula to calculate the volume of cylinder (oblique) is the same as that of a right circular cylinder. Thus, the volume (V) of an oblique cylinder whose base radius is 'r' and whose height is 'h' is,
V = πr2h
Formula to Calculate Volume of an Elliptic Cylinder
We know that an ellipse has two radii. Also, we know that the area of an ellipse whose radii are 'a' and 'b' is πab. Thus, the volume of an elliptic cylinder is,
V = πabh
Here,
- 'a' and 'b' are the radii of the base (ellipse) of the cylinder.
- 'h' is the height of the cylinder.
- π is a constant whose value is either 22/7 (or) 3.142.
Volume of a Right Circular Hollow Cylinder Formula
As a right circular hollow cylinder is a cylinder that consists of two right circular cylinders bounded one inside the other, its volume is obtained by subtracting the volume of the inside cylinder from that of the outside cylinder. Thus, the volume (V) of a right circular hollow cylinder is,
V = π(R2 - r2)h
Here,
- 'R' is the base radius of the outside cylinder.
- 'r' is the base radius of the inside cylinder.
- 'h' is the height of the cylinder.
- π is a constant whose value is 22/7 (or) 3.142.
How To Find the Volume of Cylinder?
Here are the steps to find the volume of cylinder:
- Identify the radius to be 'r' and height to be 'h' and make sure that they both are of the same units.
- Substitute the values in the volume formula V = πr2h.
- Write the units as cubic units.
Example: Find the volume of a right circular cylinder of radius 50 cm and height 1 meter. Use π = 3.142.
Solution:
The radius of the cylinder is, r = 50 cm.
Its height is, h = 1 meter = 100 cm.
Its volume is, V = πr2h = (3.142)(50)2(100) = 785,500 cm3.
Note: We need to use the formula to find the volume of a cylinder depending on its type as we discussed in the previous section. Also, assume that a cylinder is a right circular cylinder if there is no type given and apply the volume of a cylinder formula to be V = πr2h.
Important Notes on Volume of Cylinder:
- The volume of a cylinder is calculated using the formula, V = πr2h, where r is the radius of its circular base and 'h' is the perpendicular distance (height) between the centres of the bases.
- If diameter (d) is given, then find the radius (r) using r = d/2 and then substitute in the above formula to find the volume of cylinder.
Volume of Cylinder Examples
-
Example 1: Find the volume of a cylindrical water tank in litres whose base radius is 25 m and whose height is 120 m. Use π = 3.14.
Solution:
The radius of the cylindrical tank is, r = 25 m.
Its height is, h = 120 m.
Using the formula of volume of cylinder, the volume of the tank is,
V = πr2h
V = (3.14)(25)2(120) = 235500 cubic meters.
The volume of a cylinder in litres is obtained by using the conversion formula 1 cubic meter = 1000 liters.
Thus, the volume of the tank in liters is: 235500 × 1000 = 235,500,000
Answer: The volume of the given cylindrical tank is 235,500,000 liters.
-
Example 2: Calculate the volume of an elliptic cylinder whose base radii are 7 inches and 10 inches, and whose height is 15 inches. Use π = 22/7.
Solution:
The base radii of the given elliptic cylinder are,
a = 7 inches and b = 10 inches.
Its height is, h = 15 inches.
Using the volume of cylinder formula, the volume of the given elliptic cylinder is,
V = πabh
V = (22/7) × 7 × 10 × 15 = 3300 cubic inches.
Answer: The volume of the given cylinder is 3,300 cubic inches.
-
Example 3: What is the volume of the cylinder with a radius of 4 units and a height of 6 units?
Solution:
Since the exact type of cylinder is not mentioned, we need to assume it is a right circular cylinder.
Radius,r = 4 units and height,h = 6 units
Volume of the cylinder, V = πr2h cubic units.
V = (22/7) × (4)2 × 6 V = 22/7 × 16 × 6
V= 301.71 cubic units.
Answer: The volume of the cylinder is 301.71 cubic units.

FAQs on Volume of Cylinder
What is the Meaning of Volume of Cylinder?
The volume of a cylinder is the amount of space in it. It can be obtained by multiplying its base area by its height. The formula to find the volume of a cylinder of base radius 'r' and height 'h' is V = πr2h.
What Is the Formula for Calculating the Volume of a Cylinder?
The formula for calculating the volume of a cylinder is V = πr2h, where
- 'r' is the radius of the base of the cylinder
- 'h' is the height of the cylinder
- π is a constant whose value is equal to approximately 3.142.
What is the Volume of a Cylinder with Diameter?
Let us consider a cylinder of radius 'r', diameter 'd', and height 'h'. The volume of a cylinder of base radius 'r' and height 'h' is V = πr2h. We know that r = d/2. By substituting this in the above formula, V = πd2h/4.
What Is the Ratio of the Volume of a Cylinder and a Cone?
Let us consider a cylinder and a cone, each with base radius 'r' and height 'h'. We know that the volume of the cylinder is πr2h and the volume of the cone is 1/3 πr2h. Thus the required ratio is 1:(1/3) (or) 3:1.
How To Calculate Volume of a Cylinder With Diameter and Height?
The volume of a cylinder with base radius 'r' and height 'h' is, V = πr2h. If its base diameter is d, then we have d = r/2. Substituting this in the above formula, we get V = πd2h/4. Thus, the formula to find the volume of a cylinder with the diameter (d) and height(h) is V = πd2h/4.
How To Find Volume of Cylinder With Circumference and Height?
We know that the circumference of a circle of radius 'r' is C = 2πr. Thus, when the circumference of the base of a cylinder (C) and its height (h) are given, then we first solve the equation C = 2πr for 'r' and then we apply the volume of a cylinder formula, which is, V = πr2h.
How To Calculate Volume of Cylinder in Litres?
We can use the following conversion formulas to convert the volume of cylinder from m3 (or) cm3 to liters.
- 1 m3 = 1000 liters
- 1 cm3 = 1 ml (or) 0.001 liters
☛ Check:
What Happens to the Volume of Cylinder When Its Radius Is Halved?
The volume of cylinder varies directly with the square of its radius. Thus, when its radius is halved, the volume becomes 1/4th.
What Happens to the Volume of Cylinder When Its Radius Is Doubled?
We know that the volume of cylinder is directly proportional to the square of its radius. Thus, when its radius is doubled, the volume becomes four times.
How Do You Find Volume of Cylinder Using Calculator?
Volume of a cylinder calculator is a machine to calculate a cylinder's volume. To calculate the volume of a cylinder using a calculator we need to provide necessary inputs to the calculator tool, such as required dimensions like radius, diameter, height, etc. Try now the volume of a cylinder calculator enter the radius and height of the cylinder in the given box of the volume of a cylinder calculator. Click on the "Calculate" button to find the volume of a cylinder. By clicking the "Reset" button you can easily clear the previously entered data and find the volume of a cylinder for different values.
☛Also Check:
What is the Area and Volume of a Cylinder?
The surface area of a cylinder is the total area or region covered by the surface of the cylinder. The surface area of a cylinder is given by two following formulas:
- The curved surface area of cylinder = 2πrh
- The total surface area of the cylinder = 2πr2+2πrh = 2πr(h+r)
The area of a cylinder is expressed in square units, like m2, in2, cm2, yd2, etc.
The volume of a cylinder is the total amount of capacity immersed in a cylinder that can be calculated using the volume of cylinder equation is V = πr2h and it is measured in cubic units.
☛ Check:
How Does the Volume of a Hollow Cylinder Change When the Height is Doubled?
The volume of a hollow cylinder formula is V = π(R2 - r2)h cubic units. According to the volume formula, we can see that volume is directly proportional to the height of the hollow cylinder. Therefore, the volume gets doubled when the height of the hollow cylinder is doubled.
What is the Volume of Cylinder in Terms of Pi?
The volume of cylinder is defined as the capacity of a cylinder which is indicated in terms of pi. The volume of a cylinder in terms of pi is expressed in cubic units where units can be m3, cm3, in3, ft3, etc.
visual curriculum