Volume of Prism
The volume of a prism is the capacity of the prism. There can be different types of prisms like a triangular prism, square prism, rectangular prism, pentagonal prism, hexagonal prism, or octagonal prism. But the method to write the formula of volume of any prism remains the same immaterial of the type of prism. The concept of writing the formula for the volume of the prism stays the same in any case. Like all three-dimensional shapes, you will learn how to calculate the volume of any type of prism. Stay tuned to learn how to use its formula using solved examples.
| 1. | What is the Volume of Prism? |
| 2. | Formula of Volume of Prism |
| 3. | How to Calculate the Volume of Prism? |
| 4. | FAQs on Volume of Prism |
What is the Volume of Prism?
The volume of a prism is defined as the amount of space a prism occupies. A prism is a solid 3-D shape that has two same faces and other faces that resemble a parallelogram. It is a polyhedron whose naming convention is influenced by the different shapes of the bases. In the case of prisms, every prism has a different base, triangular prism (triangular base), square prism (square base), rectangular prism (rectangular base), pentagonal prism (pentagonal base), hexagonal prism (hexagonal base), or an octagonal prism (octagonal base). Thus, as each prism is a three-dimensional shape, the volume of every prism also lies in a three-dimensional plane. The unit of volume of a prism is given as cubic meters, cubic centimeters, cubic inches or cubic feet, etc.
Formula of Volume of Prism
The formula for the volume of a prism is given by the product of the area of the base and height of the prism.
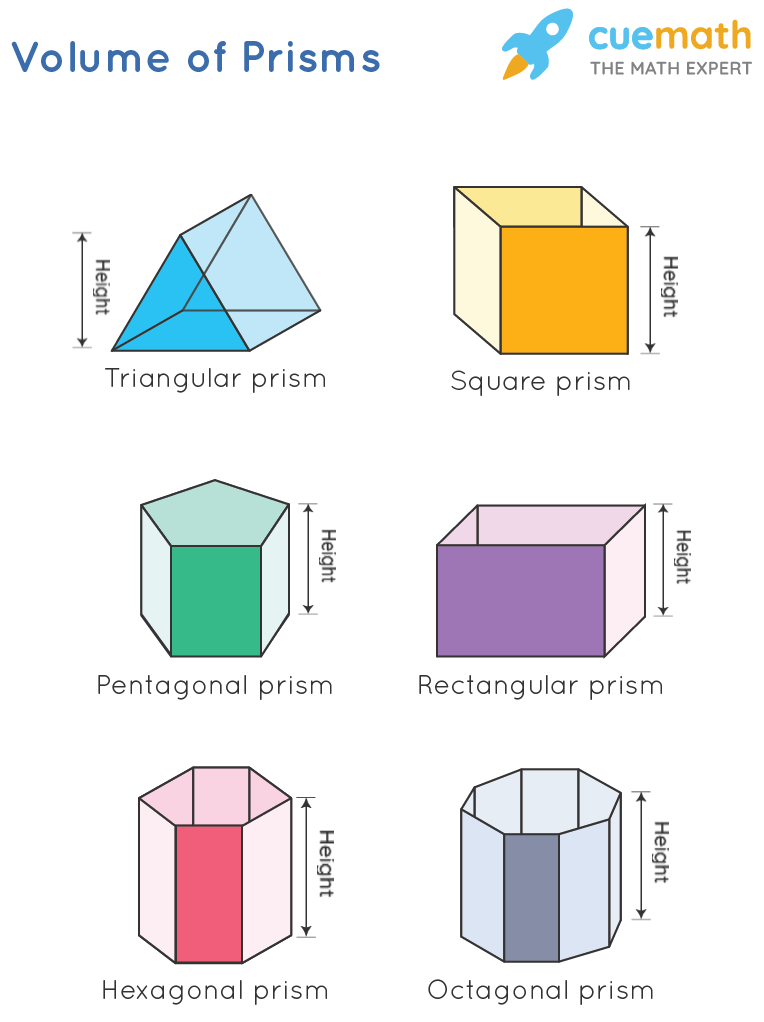
Thus, as the bases of different types of prisms are different so are the formulas to determine the volume of the prism. Look at the table below to understand this concept better:
| Shape | Base | Volume of Prism = Base area × height |
|---|---|---|
| Triangular Prism | Triangular | Volume of triangular prism = Area of triangle × height of the prism |
| Square Prism | Square | Volume of square prism = Area of square × height of the prism |
| Rectangular Prism | Rectangular | Volume of rectangular prism = Area of rectangle × height of the prism |
| Trapezoidal Prism | Trapezoidal | Volume of trapezoidal prism = Area of trapezoid × height of the prism |
| Pentagonal Prism | Pentagonal | Volume of pentagonal prism = Area of pentagon × height of the prism |
| Hexagonal Prism | Hexagonal | Volume of hexagonal prism = Area of hexagon × height of the prism |
| Octagonal Prism | Octagonal | Volume of octagonal prism = Area of octagon × height of the prism |
Thus, the volume of a prism can be given as V = B × H where V is the volume, B base area, and H height of the prism. The unit of base area is given in square units and the height of the prism is given in units. Thus, the unit of volume of the prism is given as V = (square units) × (units) = cubic units.
How to Calculate the Volume of Prism?
The steps to determine the volume of the prism are:
- Step 1: Write the given dimensions of the prism.
- Step 2: Determine the volume of the prism using the formula V = B × H where V, B, and H are the volume, base area, and height of the prism.
- Step 3: The value of the volume of the prism is once obtained then add the unit of volume of prism in the end (in terms of cubic units).
Example: Find the volume of a prism whose base area is 3 square inches and height is 7 inches.
Solution: As we know, the volume of the prism is V = B × H.
Given that: B = 3 square inches, H = 7 inches
Thus, the Volume of the prism, V = B × H ⇒ V = 3 × 7 = 21 in3
Therefore, the volume of the prism is 21 cubic inches.
Important Notes
- The volume of any prism depends on the shape of its base. With the change in the shape of the base, the area of the base changes as well.
Volume of Prism Examples
-
Example 1: What is the base area of the prism if the volume of the prism is 324 cubic units and the height of the prism is 9 units.
Solution:
The given dimensions are the volume of the prism = 324 cubic units and the height of the prism = 9 units. Let the base area of the prism be "B".
Substituting the values in the volume of the prism formula, Volume of prism = V = B × H = 324 cubic units
⇒ 9B = 324
⇒ B = 36 square unitsTherefore, the base area of the prism is 36 square units.
-
Example 2: Find the height of the prism if the volume of the prism is 729 cubic units and the base area is 27 square units.
Solution:
The given dimensions are the volume of the prism = 729 cubic units and the base area of prism = 27 square units. Let the height of the prism be "H".
Substituting the values in the volume of the prism formula, Volume of prism = V = B × H = 729 cubic units
⇒ 27H = 729
⇒ H = 27 unitsTherefore, the height of the prism is 27 units.

FAQs on Volume of Prism
What is the Definition of the Volume of a Prism?
The amount of space occupied by a prism is referred to as the volume of a prism. The volume of the prism depends on the base radius of the prism and the height of the prism. The unit of volume of the prism is expressed in m3, cm3, in3, or ft3.
What is the Formula for Volume of Prism?
The formula for the volume of a prism is obtained by taking the product of the base area and height of the prism. The volume of a prism is given as V = B × H where, "V" is the volume of the prism, "B" is the base area of the prism, and "H" is the height of the prism.
How to Find the Volume of Prism?
We can find the volume of the prism using the following steps:
- Step 1: First write the given dimensions of the prism.
- Step 2: Find the volume of the prism using the formula V = B × H where "V", "B", and "H" are the volume, base area, and height of the prism.
- Step 3: Once the value of the volume of the prism is obtained, write the unit of volume of prism in the end (in terms of cubic units).
How Do You Find the Base Area of Prism if the Volume of Prism is Given?
The steps to determine the base area of the prism, if the volume of the prism is given, are:
- Step 1: Write the given dimensions of the prism.
- Step 2: Substitute the given values in the formula V = B × H where "V", "B", and "H" are the volume, base area, and height of the prism.
- Step 3: Now solve the equation for "B".
- Step 3: Once the value of the base area of the prism is obtained, write the unit of the base area prism in the end (in terms of square units).
What Happens to the Volume of Prism if the Base Area of Prism is Doubled?
The volume of the prism depends on the base radius of the prism. Thus, the volume of the prism doubles if the base area of the prism is doubled as "B" is substituted by "2B" as V = (2B) × H = 2 (B × H) which is double the original volume of the prism.
What Happens to the Volume of Prism When the Base Area and Height are Doubled?
The volume of the prism will quadruple the original volume if the base area and height of the prism are doubled as, radius, "B" is substituted by 2B, and height, "H" is substituted by 2H. Thus, V = (2B) × (2H) = 4 (B × H) which is four times the original volume of the prism.
How Does the Volume of Prism Change if the Type of Prism Changes?
The volume of the prism depends on the base area of the prism. As the type of prism changes, the base of the prism changes thereby changing the base area of the prism. This change in the base area of the prism changes the volume of the prism.
visual curriculum