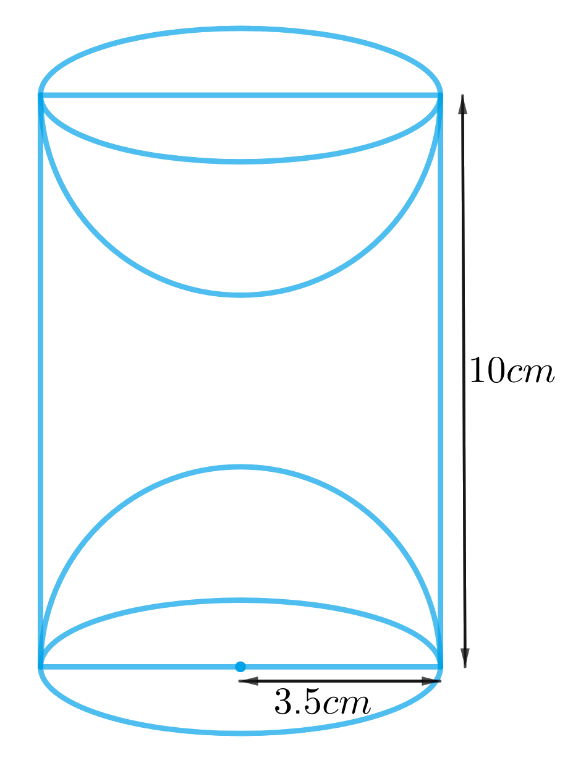
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 13.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article

Solution:

From the figure, it can be seen that the radius of the hemispheres scooped out is the same as the radius of the base of the cylinder since both the hemispheres are of equal radius.

Therefore, the total surface area of the article only includes the CSA of both the hemispheres and the cylinder.

TSA of the article = 2 × CSA of the hemispherical part + CSA of the cylindrical part.

We will find the TSA of the article by using formulae;

CSA of the hemisphere = 2πr², where r is the radius of the hemisphere.

CSA of the cylinder = 2πrh, where r and h are the radius and height of the cylinder respectively.

Height of the cylinder = h = 10 cm

Radius of the cylinder = radius of the hemisphere = r = 3.5 cm

TSA of the article = 2 × CSA of the hemispherical part + CSA of the cylindrical part

= 2 × 2πr² + 2πrh

= 2πr (2r + h)

= 2 × 22/7 × 3.5 cm × (2 × 3.5 cm + 10 cm)

= 22 cm × 17 cm

= 374 cm²

Thus, the total surface area of the article is 374 cm².

☛ Check: NCERT Solutions for Class 10 Maths Chapter 13

Video Solution:

A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 13.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
 

NCERT Solutions Class 10 Maths  Chapter 13 Exercise 13.1 Question 9 

Summary:

A wooden article was made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, the total surface area of the wooden article is 374 cm².

☛ Related Questions:

• 2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
• A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
• A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
• A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.