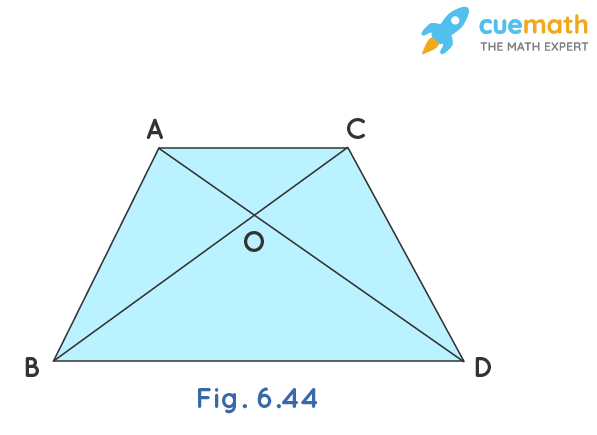
In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that area(ABC) / area(DBC) = AO/DO

Solution:

In ΔABC, draw AM ⊥ BC

In ΔDBC, draw DN ⊥ BC

Now,

In ΔAOM and ΔDON

∠AMO = ∠DNO = 90 °

∠AOM = ∠DON (Vertically opposite angles)

⇒ ΔAOM ~  ΔDON (AA criterion)

⇒ AM / DN = OM / ON = AO / DO.............. (1)

Now,

Area of ΔABC = 1/2 × base × height = 1/2 × BC × AM

Area of ΔDBC = 1/2 × BC × DN

Area of ΔABC / Area of ΔDBC = (1/2 × BC × AM) / (1/2 × BC × DN)

Area of ΔABC / Area of ΔDBC = AM/DN

Thus, Area of ΔABC / Area of ΔDBC = AO/DO  [From equation (1)]

☛ Check: NCERT Solutions for Class 10 Maths Chapter 6

Video Solution:

In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that area( ABC) / area(DBC) = AO/DO.

NCERT Class 10 Maths Solutions Chapter 6 Exercise 6.4 Question 3

Summary:

In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, we have proved that area( ABC)/area(DBC) = AO/DO.

☛ Related Questions:

• If the areas of two similar triangles are equal, prove that they are congruent.
• D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ ABC. Find the ratio of the areas of ∆ DEF and ∆ ABC
• Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
• Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.