NCERT Solutions Class 10 Maths Chapter 8 Exercise 8.4 Introduction to Trigonometry
NCERT solutions for class 10 maths chapter 8 exercise 8.4 Introduction to Trigonometry targets one of the most important sections of this chapter on trigonometric identities. It not only carries the maximum weightage in board exams but simplifies solving problems several fold. An equation involving trigonometric ratios of an angle is called a trigonometric identity if it is true for all values of the angles involved. These identities will make their way throughout the remainder of a child’s school career. The NCERT solutions exercise 8.4 class 10th has a total of 5 questions with subparts that are based on proving expressions using the identities that kids have learned.
To solve NCERT solutions of ex 8.4 class 10th, students must revise all the concepts from the previous three exercises. A fun fact to note is that using these identities, we can express each trigonometric ratio in terms of other trigonometric ratios, i.e., if any one of the ratios is known, we can also determine the values of other trigonometric ratios. One can refer to the detailed solution set of class 10 maths NCERT solutions chapter 8 exercise 8.4 Introduction to Trigonometry with the help of the PDF link mentioned below:
☛ Download NCERT Solutions Class 10 Maths Chapter 8 Exercise 8.4
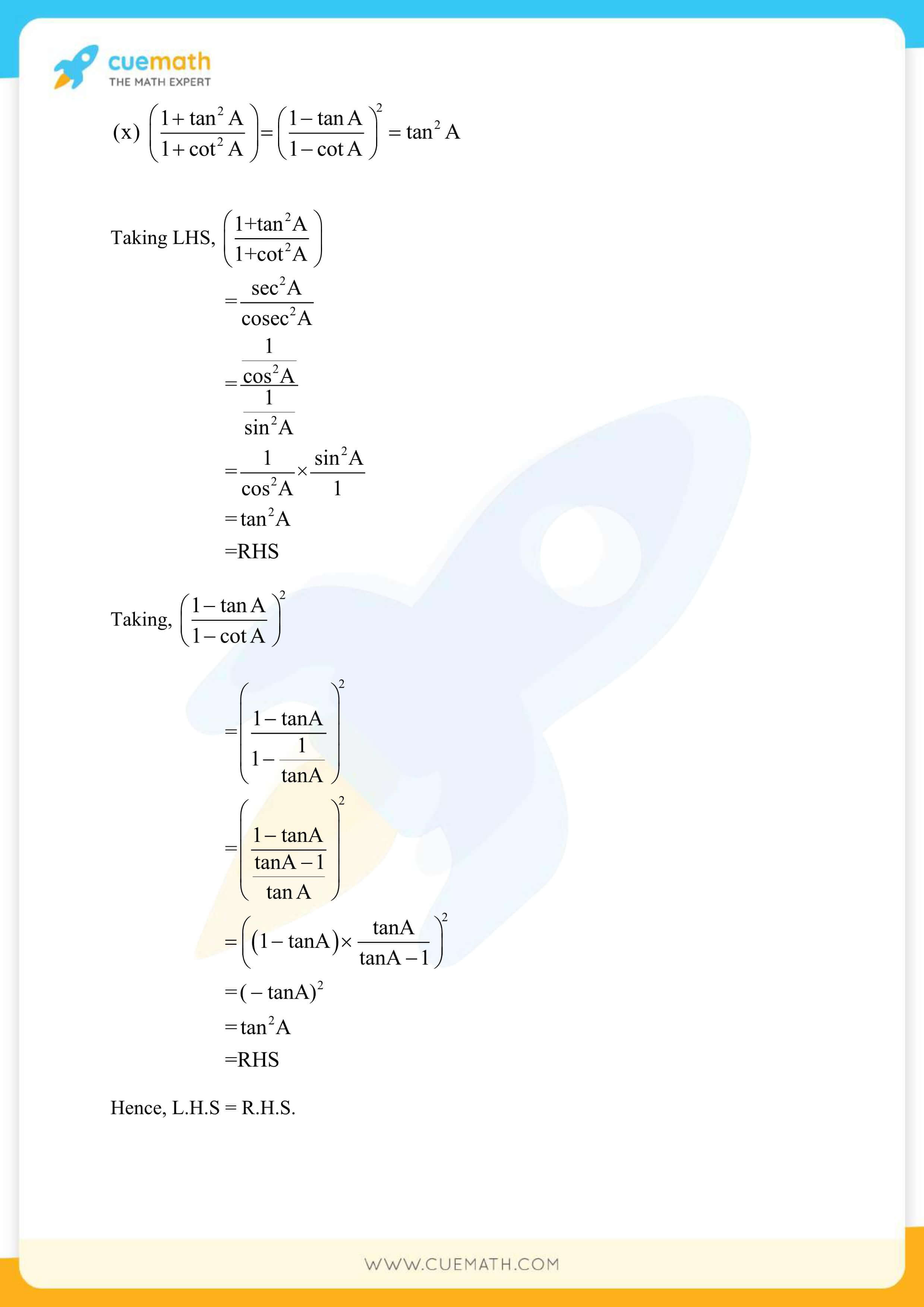
Exercise 8.4 Class 10 Chapter 8















Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
More Exercises in Class 10 Maths Chapter 8
- NCERT Solutions Class 10 Maths Chapter 8 Ex 8.1
- NCERT Solutions Class 10 Maths Chapter 8 Ex 8.2
- NCERT Solutions Class 10 Maths Chapter 8 Ex 8.3
NCERT Solutions Class 10 Maths Chapter 8 Exercise 8.4 Tips
NCERT solutions class 10 maths chapter 8 exercise 8.4 Introduction to Trigonometry revolves around proving questions using trigonometric identities. Since there are a lot of such questions, students need to have a crystal clear understanding of the formulas, their derivations, and their origin. This implies that it is important for kids to go through the proof of all identities with laser focus.
NCERT solutions class 10 maths chapter 8 exercise 8.4 is all about conceptual understanding. There are a few twisted sums that students might find difficult, but it is all about finding the key point that can lead you to the answer. Kids can refer to their formula and value chart from the previous exercises and seek help from teachers if needed while attempting the questions.
Download Cuemath NCERT Solutions PDF for free and start learning!
NCERT Class 10 Maths Video Solutions Chapter 8 Exercise 8.4
| NCERT Videos for Class 10 Maths Chapter 8 Exercise 8.4 | |
|---|---|
| Question 1 | Question 4 |
| Question 2 | Question 5 |
| Question 3 | |
FAQs on Ex 8.4 Class 10th
Where Can I find the Solutions of Exercise 8.4 Class 10th?
The solutions of ex 8.4 class 10th can be found on this page. Scroll up to find a PDF of solutions for exercise 8.4 of class 10 maths.
How Many Exercises are there in Chapter 8 in Class 10th?
Class 10th Chapter 8 deals with and it has 4 exercises. 8.1 has 11 questions, 8.2 has 4 questions, 8.3 has 7 questions, and class 10th math 8.4 has 5 questions.
How Many Questions Does Cass 10 maths Chapter 8 Exercise 8.4 Has?
In class 10 maths chapter 8 exercise 8.4, there are 5 questions some of which again have subparts.
- Question 3 has 2 subparts.
- Question 4 has 4 subparts.
- Question 5 has 10 subparts.
What is Class10 Maths Ex 8.4 All about?
Class 10 maths ex 8.4 is all about trigonometric identities. The basic trig identities are cosec A = 1/sin A; sec A = 1/cos A; cot A = 1/tan A; sin2A + cos2A = 1; cosec2A - cot2A = 1; sec2A - tan2A = 1. Using these identities, we have to establish/prove the given identities in exercise 8.4 of class 10.
visual curriculum