Sequence Formulas

We have two types of sequence formulas, arithmetic sequence formulas, and geometric sequence formulas. An arithmetic sequence is a sequence in which the difference between every two consecutive terms is constant. A geometric sequence is a sequence in which the ratio of every two consecutive terms is constant. Let us learn the sequence formulas in detail along with a few solved examples here.

What Are Sequence Formulas?

The sequence formulas include the formulas of finding the n^th term and the sum of the first n terms of each of the arithmetic sequence and geometric sequence. Here are the sequence formulas which will in detail be explained below the list of formulas.

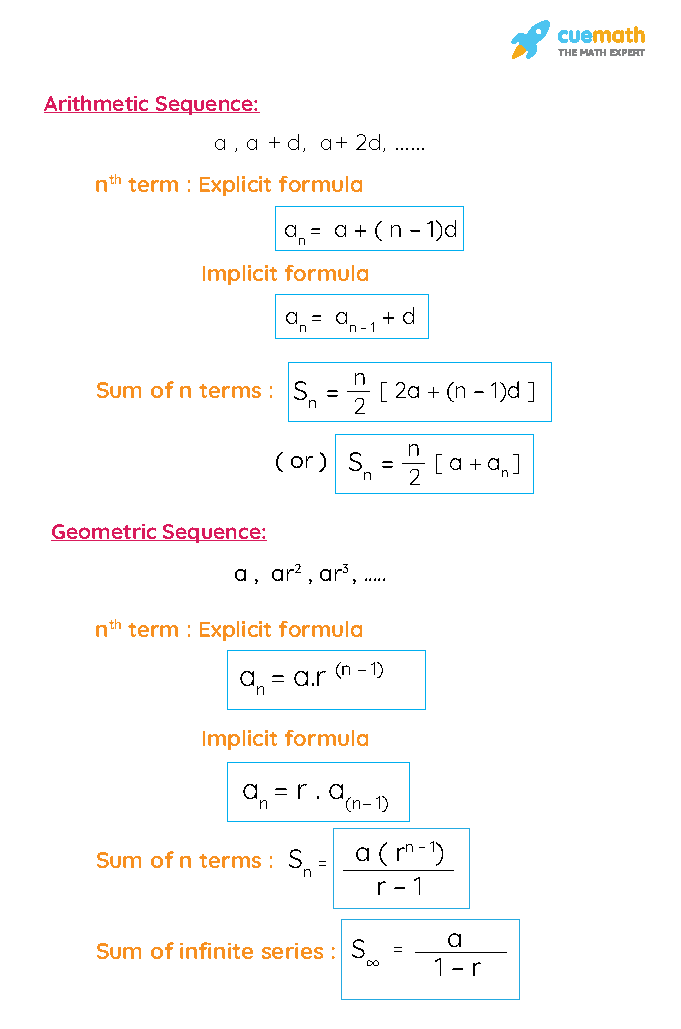
Arithmetic Sequence Formulas

Let us consider the arithmetic sequence a, a + d, a + 2d, ... where the first term is 'a' and the common difference is 'd'. Here are the formulas related to the arithmetic sequence.

• n^th term of arithmetic sequence (explicit formula) is, \(a_n\) = a + (n - 1) d.
• n^th term of arithmetic sequence (implicit formula) is, \(a_n\) = \(a_{n-1}\) + d.
• The sum of n terms of arithmetic sequence is, \(S_n\) = (n/2) [ 2a + (n - 1) d ] (OR) \(S_n\) = (n/2) [a + \(a_n\)]
  Here, \(a_n\) is the last term of the sequence.

Both explicit and implicit formulas are used to find the n^th term of an arithmetic sequence. Among them, we use the explicit formula when the values of 'a', 'n', and 'd' are known and we use the implicit formula when we know only the previous term and the common difference.

Geometric Sequence Formulas

Let us consider the geometric sequence a, ar, ar², ... where the first term is 'a' and the common difference is 'd'. Here are the formulas related to the geometric sequence.

• n^th term of geometric sequence (explicit formula) is, \(a_n\) = a · r^{n - 1}.
• n^th term of geometric sequence (implicit formula) is, \(a_n\) = \(a_{n-1}\) · r.
• The sum of n terms of geometric sequence is, \(S_n\) = a (rⁿ - 1) / (r - 1).
• The sum of infinite terms of geometric sequence (when |r| < 1) is, \(S_n\) = a / (1 - r).

Both explicit and implicit formulas are used to find the n^th term of a geometric sequence. Among them, we use the explicit formula when the values of 'a', 'n', and 'r' are known and we use the implicit formula when we know only the previous term and the common ratio.

Note: We can learn the other important formulas related to sequences by clicking here.

We can see the applications of sequence formulas in the section below.

Solved Examples on Sequence Formulas

Example 1: Find the 17^th term in the arithmetic sequence 5, 1, -3, ...

Solution:

The first term is, a = 5.

The common difference is, d = 1 - 5 = -3 -1 = ... = -4.

The sequence formula to find n^th term of an arithmetic sequence is,

\(a_n\) = a + (n - 1) d

To find the 17^th term, we substitute n = 17 in the above formula.

\(a_{17}\) = 5 + (17 - 1) (-4) 

= 5 + (16)(-4)

= 5 - 64

= -59

Answer: The 17^th term of the given sequence = -59.

Example 2: Using a suitable sequence formula, find the sum of the sequence (1/5) + (1/15) + (1/45) + ....

Solution:

We can see that the given sequence is geometric as the ratio of every two consecutive terms is constant. i.e.,

Common ratio, r = (1/15) / (1/5) = (1/45) / (1/15) = ... = 1/3.

The first term is, a = 1/5.

Since the sequence is infinite, we will use the sum of infinite terms of a geometric sequence formula here to find the sum.

\(S_n\) = a / (1 - r) [since r < 1]

= (1/5) / (1 - (1/3) )

= (1/5) / (2/3)

= 3 / 10

Answer:  The sum of the infinite terms of the given sequence = 3 / 10.

Example 3: Find the 15^th term of the geometric sequence 1, -3, 9, -27, ...

Solution:

The first term is a = 1.

The common ratio is, r = -3/1 = 9/(-3) = (-27)/9 = ... = -3.

Using the sequence formula, the n^th term of a geometric sequence is,

\(a_n\) = a · r^{n - 1}

To find the 15^th term, we substitute n = 15 in the above formula. Then we get:

\(a_{15}\) = 1 (-3)^{15 - 1} = (-3)¹⁴ =  4,782,969

Answer: The 15^th term of the given geometric sequence = 4,782,969.